EMT 668 - ASSIGNMENT 10
Parametric Curves
by
Kimberly N. Bennekin
EXPLORATIONS
Graph
x = cos(t)
y = sin(t)
for t within the interval [0,2pi].
How would you change the parametric equations to explore other graphs?
First let us consider the original parametric curve for t within the interval
[0,2Pi]:
x = cos (t)
y = sin (t)
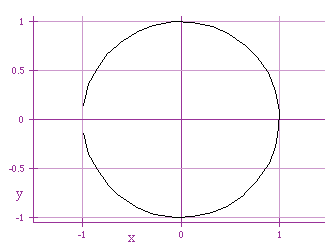
We can consider a number of variations to this curve. First let us consider
multiplying our parameter t by a constant in both x = cos
(t) and y = sin (t). Let's consider 2, 3 and -1.
x = cos (2 t)
y = sin (2 t)
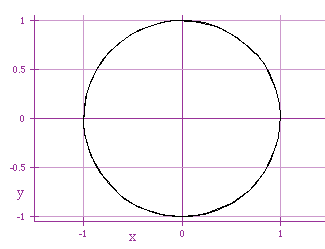
x = cos (3 t)
y = sin (3 t)
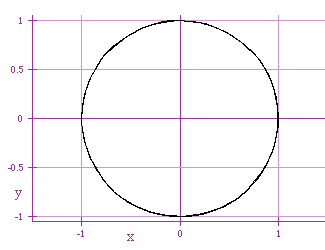
x = cos (- t)
y = sin (- t)
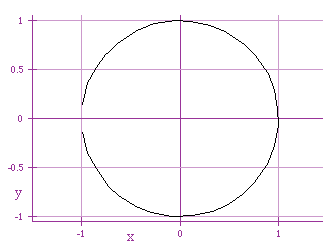
Let us consider putting multiples on only one of
the funtions.
x = cos (2 t)
y = sin (t)
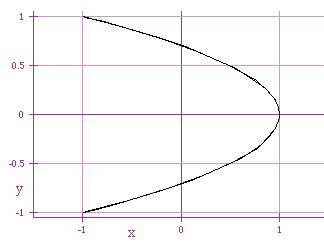
x = cos (3 t)
y = sin (t)
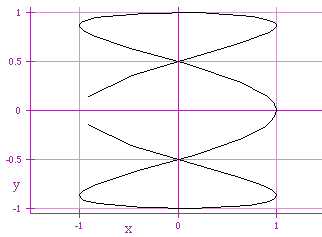
x = cos (4 t)
y = sin (t)
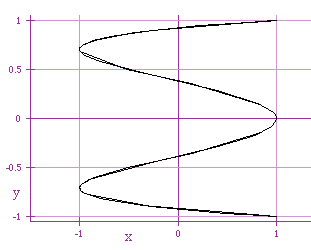
x = cos (5 t)
y = sin (t)
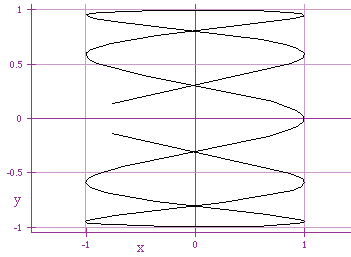
It seems that the constant multiple within x = cos (a t), for
even a, creates additional dips in our graph. For odd a, we
create additional complete cycles in the graph.
Multiplying by a constant within y = sin (a t) will
have a different effect. Consider the following graphs.
x = cos (t)
y = sin (2 t)
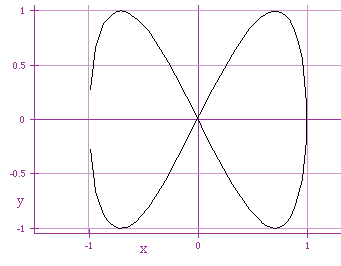
x = cos (t)
y = sin (3 t)
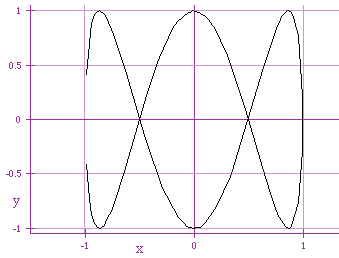
This manipulation creates a "Bow Tie" graph. The larger
the constant multiple, the more rotations we have.
Let's consider the addition of a constant to t. We
will not consider a parametric curve where the change in both x = cos
(t) and y = sin (t) are the same. Consider the following graphs:
x = cos (t+1)
y = sin (t)
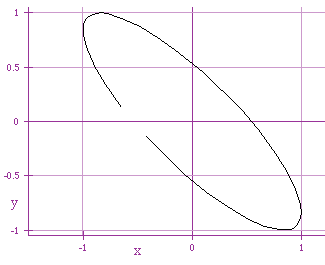
x = cos (t+2)
y = sin (t)
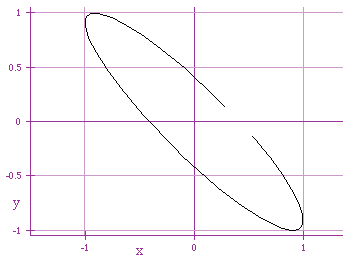
x = cos (t-1)
y = sin (t)
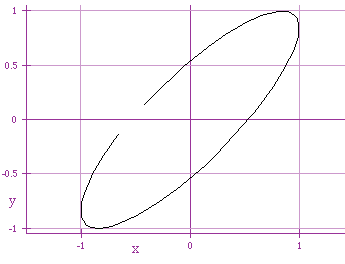
By adding or subtracting a constant to t within x = cos (t
+ a), we create an ellipse. This investigation leads me to believe,
the larger the constant you add to t, the narrower your ellipse becomes.
Subtracting a constant reflects the graph about the y-axis.
Let's consider adding and subtracting a constant to t
within y = sin (t +a). Consider the following:
x = cos (t)
y = sin (t+1)
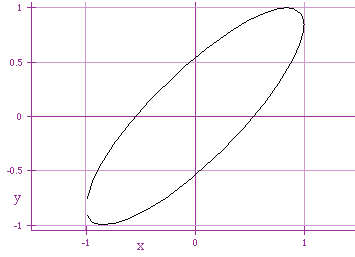
x = cos (t)
y = sin (t-1)
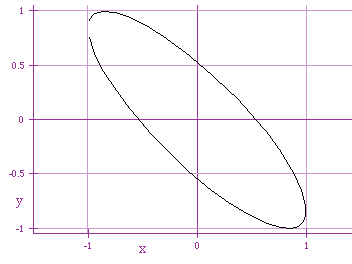
It seems that adding 1 within y = sin (t+a) has the same effect
as subtracting 1 within
x = cos (t - a) and subtracting 1 within y = sin (t - a) has
the same effect as adding 1 within
x = cos (t+ a).
These are just a few of the many explorations that can be done on this set
of parametric equations.















