EMT 668 - Algorithms & Computers
ASSIGNMENT 2, #6
by
Kimberly N. Bennekin
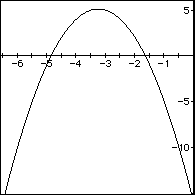
The following is the graph of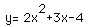 
.
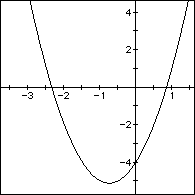
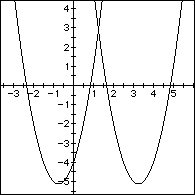
i) Overlay a new graph replacing each x by (x - 4). The following is the
graph of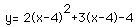 
(right) and 
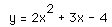(left).
ii) Change the equation to move the graph into the second quadrant.
The standard form for the equation of a parabola is
,
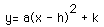where (h,k) is the vertex of the parabola. To move the graph into the
second quadrant, we would have to move the vertex into the second quadrant
by making h<0 and k>0. If we write
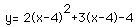
in standard form we get
,
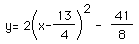where the vertex is (13/4, -41/8) which lies in Quadrant IV. To move
the vertex into Quadrant II, we change the equation to
,
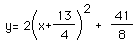which moves the vertex of the parabola to (-13/4, 41/8).
The graph of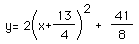 
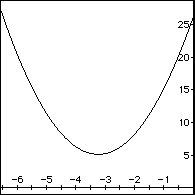
iii) Change the equation to produce a graph concave down that shares
the same vertex.
If a>0, the parabola is concave up. If a<0, the parabola
is concave down. If we take the identical
equation and change a from 2 to -2, we will flip the parabola down.
This will not change the vertex.
The graph of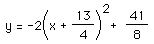 
.
