EMT 668 - ASSIGNMENT 9
Pedal Triangles
by
Kimberly N. Bennekin
Let triangle ABC be any triangle. Then if P is any point in the plane,
then the triangle formed by constructing perpendiculars to the sides of
ABC (extended if neccessary) locate three points R, S, and T that are the
intersections. Triangle RST is the Pedal Triangle for the Pedal Point P.
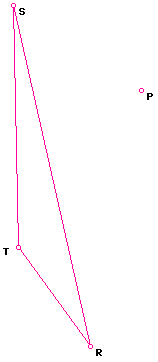
Use GSP to create a script for the general construction of a pedal triangle
RST where P is any point in the plane of ABC.
What if the Pedal point is chosen to be one of the sides of the triangle?
Consider the following:
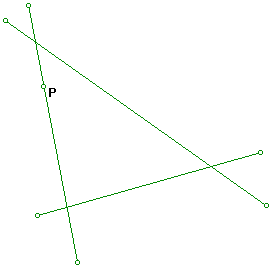

A vertex of the Pedal triangle occurs at the Pedal point.
What if the Pedal point is chosen as one of the verticies of the triangle
ABC? Consider the following:
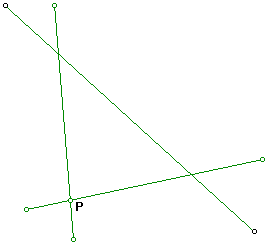
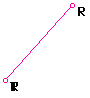
If the Pedal point is a vertex of the triangle ABC, then a pedal triangle
does not exist. It is just a line segment.
Many explorations can be made
with Pedal triangles using the script shown above and GSP.





