Triangle Inequalities Unit
By the end of this unit, students should understand and be able to use the triangle inequality, side-angle inequality and exterior angle inequality.
Lesson One: Triangle Inequality
Students will be given the Triangle Inequality GSP file. They should use the file to complete the worksheet shown below.

After working through the GSP file and worksheet, students should answer the following questions:
1. Why was it impossible to construct a triangle with some of the given lengths?
2. Write a conjecture about the relationship among the lengths of the three sides of a triangle.
Students should be instructed that the conclusion they should arrive at is called the Triangle Inequality: The sum of the lengths of two sides of a triangle must be greater than the length of the third side. [Note: Students will need guidance from the teacher to arrive at the conclusion.]
Lesson Two: Proof and Application of the Triangle Inequality
Students should be reminded of the conclusion they made from the previous lesson. This lesson will seek to prove that the Triangle Inequality is true for any triangle. In order to complete the proof, students should be reminded of the fact that the shortest distance from a point to a line is the line perpendicular to the line through the point.
PROOF ACTIVITY:
Given any triangle ABC and all three altitudes, we want to prove 1) BA + AC > BC, 2) BA + BC > AC, and 3) AC + BC > AB.
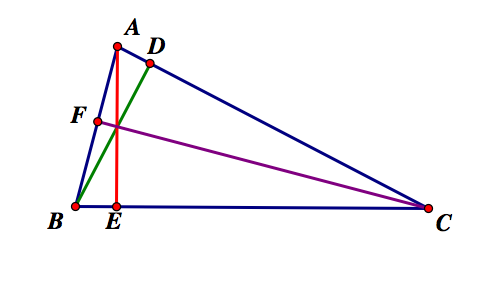
Let's first show that BA + AC > BC.
BE is the shortest distance from B to AE. So, BA > BE.
Similarly, CE is the shortest distance from C to AE. So, AC > CE.
Adding the inequalities yields BA + AC > BE + CE.
We know the BE + CE = BC.
Therefore, BA + AC > BC.
The final two cases will be left as exercises for the students.
NOTE: Students should understand that the above proof is valid for acute triangles.
Next, students will be shown the Euclidean proof.
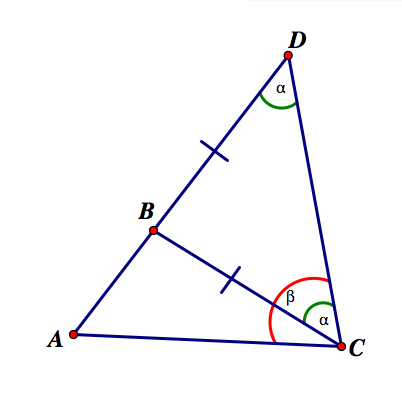

Students should be asked: Can you prove that BC + CA > AB and that AB + AC > BC? Is it necessary to prove these two cases? Explain your answer.
APPLICATION:
Students should solve the following problems:
1. The lengths of three sides of a triangle are 12, 15 and x. What is the greatest possible integer value for x? What is the smallest possible integer value for x?
2. The lengths of two sides of a triangle are 7 and 12. Find the range of possibilities for the length of the third side.
3. Two sides of an isosceles triangle measure 3 and 7. Which of the following could be the measure of the third side: 9, 7, or 3?
Lesson Three: Exterior Angle Inequality
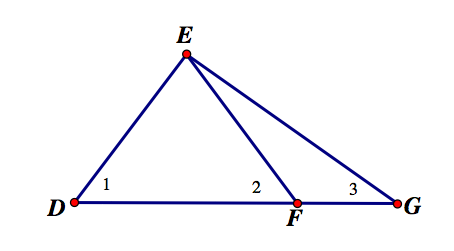
Before getting started, students should be reminded of the Exterior Angle Theorem, which states that the measure of angle 3 = measure of angle 1 + measure of angle 2. (See image below.)
Using GSP, students should construct any scalene triangle ABC. Students should measure the angles labeled 1, 2 and 3.

Ask the students to compare the measures of angles 1 and 3.
By the Exterior Angle Theorem, the measure of angle 3 = measure of angle 1 + measure of angle 2.
Therefore, the measure of angle 3 > measure of angle 1.
Ask the students to compare the measures of angles 2 and 3.
Again, by the Exterior Angle Theorem, the measure of angle 3 = measure of angle 1 + measure of angle 2.
Therefore, the measure of angle 3 > measure of angle 2.
So, angle 3 is greater than both angle 1 and angle 2.
As an exercise, students will work in groups to complete a proof of the Inequality. The GSP file will be provided to get students started.
Lesson Four: Side Angle Inequality
Using GSP, students should construct any scalene triangle ABC, such that AB is the longest side and AC is the shortest side. Then, students should measure each side and angle.
Students should answer the following questions:
1. Describe the relationship between the location of the longest side and the location of the largest angle of ABC.
2. Describe the relationship between the location of the shortest side and the location of the smallest angle of ABC.
3. Can you make a conjecture about the relationship between the length of a side and the angle opposite it?
Students should arive at the conclusion that in a triangle, the longest side must be opposite the largest angle, and the shortest side must be opposite the smallest angle. This is called the Side Angle Inequality. Next, students should work through the following proof. Prior to beginning the proof, students should be reminded of the Exterior Angle Inequality from the previous lesson.
PROOF:
Let ABC be a triangle in which side AC is longer than side BC. We want to show that angle ABC is greater than angle BAC.
Next, construct point D on side AC such that CD is congruent to CB. (Since BC is shorter than AC, we know that point D will lie between points A and C.) Construct segment BD. Because this segment is inside angle ABC, angle ABC is greater than angle DBC. Then, angle DBC is congruent to angle BDC since they are the angles at the base of an isosceles triangle.
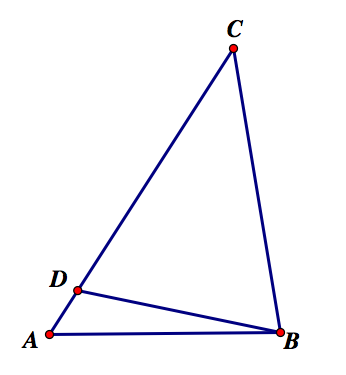
Then, since BDC is the exterior angle of triangle ABD, it is greater than both angles DAB and DBA. We also know that angle DAB is congruent to angle CAB since they are the same angle. Therefore, angle BDC is greater than angle CAB.
So, we have that angle ABC > angle DBC; angle DBC = angle BDC; and angle BDC > angle BAC.
Therefore, angle ABC > angle BAC.
So, the larger angle ABC is opposite the longer side AC.
Lesson Five: Applications of the Exterior Angle and Side Angle Inequalities
APPLICATION:
Students should solve the following problems:
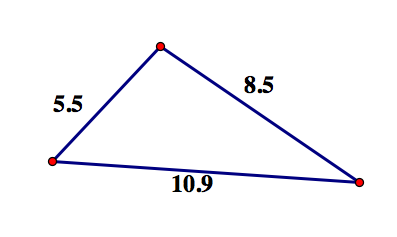
1. The figure below shows a triangle with sides of different measures. List the angles of this triangle in increasing order by their measure.
2. The figure below shows triangle ABC. Which side must be the longest? Explain your answer

3. Given that triangle DEF is isosceles, with base DF, prove that EG > ED. You can assume that the segment joining points D and G is straight.
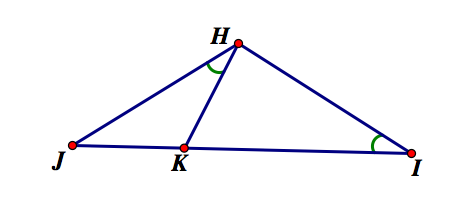
4. In the figure below, angle JHK is congruent to angle HIK. Prove that the measure of angle JKH is greater than the measure of angle JHK.