
Assignment 2:
Adventures with Quadratics
Examining2+f.gif)
![]()
By: Bennett Lewis
We are going to explore the graph of the following equation and its properties:
![]() .
.
First, let's examine the graph when d=f=1.
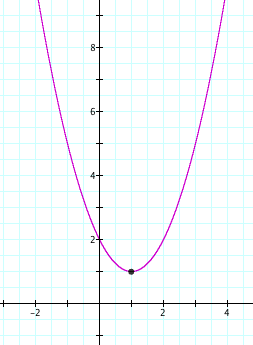
Notice we have a parabola with the vertex (1,1). How do you think the vertex correlates to our equation?
Let's keep exploring other graphs, varying d and f, and see what we discover.
First, let's fix f at f=1 and vary d. What do you expect will happen?
Notice the following graph with corresponding equations:
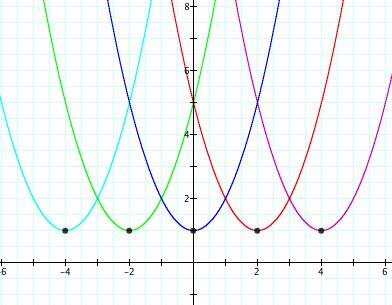
What are the vertices of the parabolas above?
Going from right to left we have (4,1), (2,1), (0,1), (-2,1), and (-4,1).
As you can see, as d changes, there is a horizontal shift in the graph of y. It is important to remember that f=1.
Now, let's examine what happens when we fix d at d=1 and vary the value of f. What do you expect will happen?
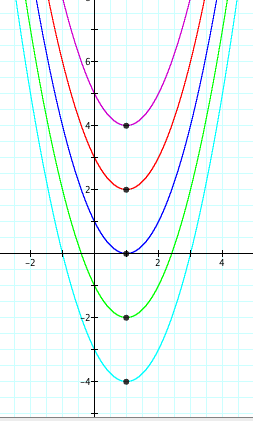
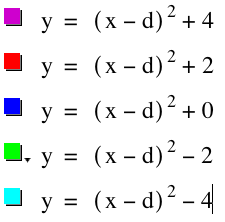
What are the vertices of the parabolas above?
Going from top to bottom, we have (1,4), (1,2), (1,0), (1,-2), and (1,-4).
As you can see, there is a vertical shift as the value of f changes. Again, it is important to notice that d is fixed at d=1.
Now that we have examined what happens when we change d and f in the equation, how can we find the vertex of the parabola in a given equation?
Let's look at another example.
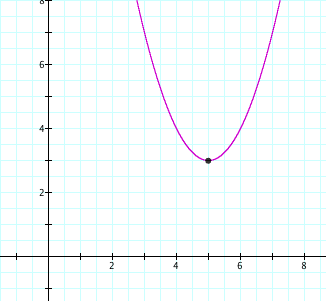
![]()
Notice that the vertex of the above parabola is (5,3).
Using what we know about the changing d and f and the graph above, we can determine that the point (d,f) is the vertex of the given equation. When d varies, there is a horizontal shift and when f varies, there is a vertical shift.
Click here to examine a video of the translations when d and f are varied. Can you tell which is which?