

The nine point circle can be found for any triangle. The nine point circle is made up of the midpoints of the sides, the feet of the altitudes, and the midpoints of the segments connecting the vertices and the orthocenter. So given any triangle, ABC.
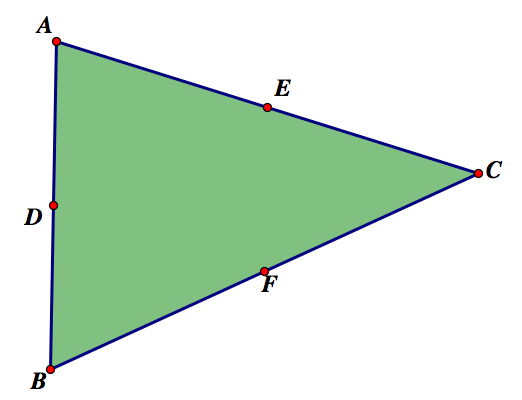
First let's find the midpoints of the sides. Let's label them D, E, and F.
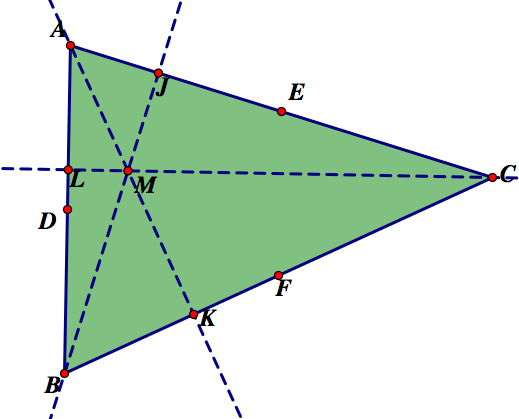
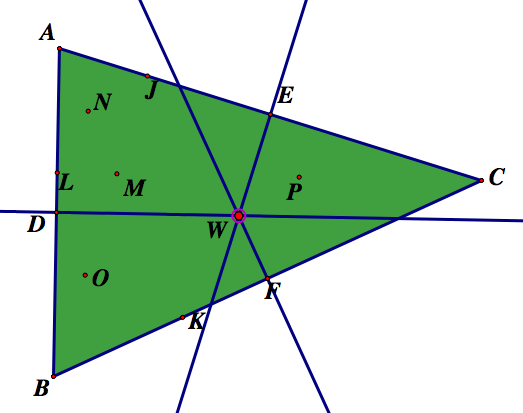
Next, we will find the altitudes of the triangle. Since the orthocenter of the triangle is the intersection of the altitudes of the triangle, we will also find the orthocenter of the triangle. We will call the feet of the altitudes L, J, K, and the orthocenter M.
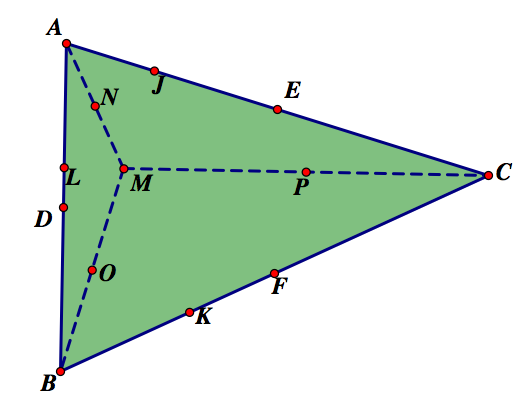
Now we will find the midpoints of the segments connecting the vertices and the orthocenter. We will label them N, O, and P.
After finding the points of the nine point circle it is necessary to find the center of the circle. To do this we will find the midpoint of the segment that connects the orthocenter and the circumcenter. The circumcenter of a triangle is the point where the perpendicular bisectors of the side intersect. Let's call the circumcenter W. We will call the center of the nine point circle X.
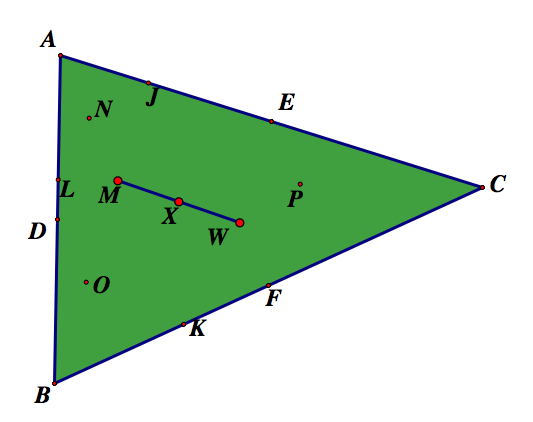
Now, the moment we've all been waiting for!!
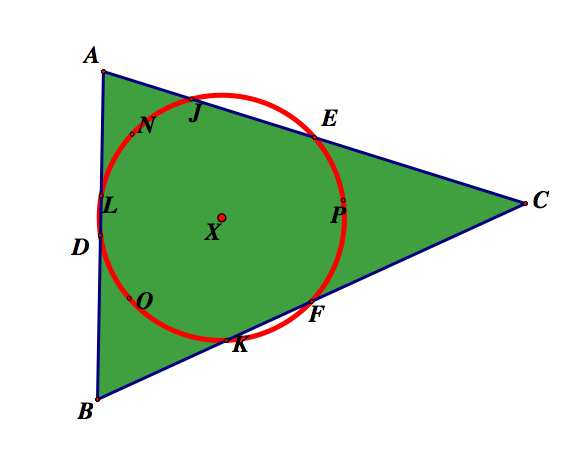
To explore the nine point circle click here!