

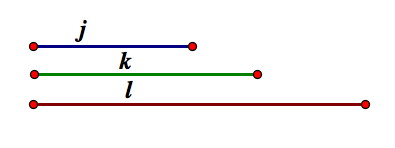
In this assignment we will construct a triangle given its medians. Below are three medians j, k, and l.
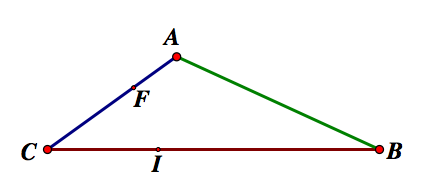
First, we will construct the triangle formed by the medians.

We want these three medians to concur at one point within the unknown triangle. We also know that they intersect at 1/3 the distance of the median. So, let's trisect two sides of the triangle, say AC and BC. We will call these points, F and I respectively.
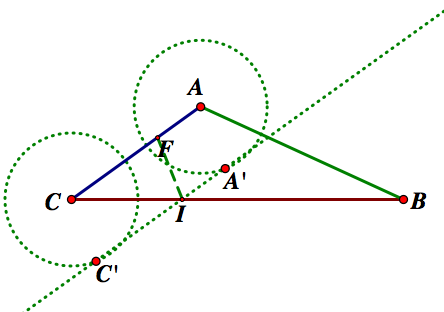
Next, we will construct a line through I parallel to AC. Then we will construct circles around A and C with a radii of FI. The intersection of these circles and the parallel line we will call A' and C' respectively.
Now, we will construct A'C'.
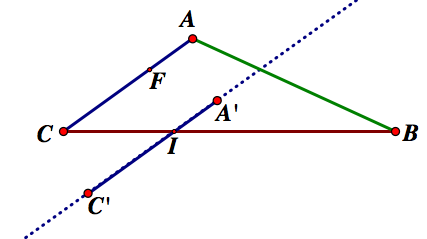
Notice that we now have two medians meeting at 1/3 the distance of each. By similar construction, we will find the other medians.
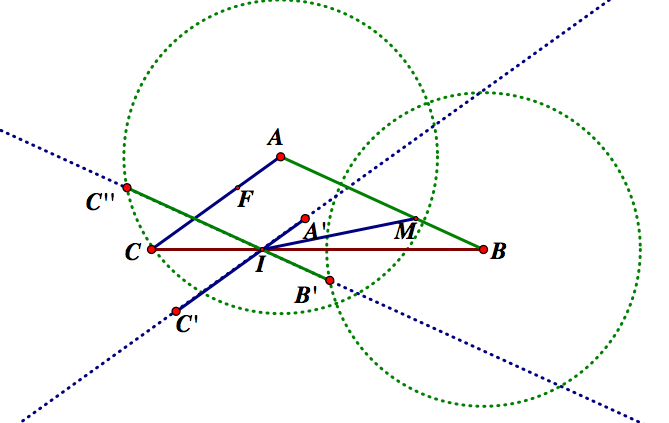
Notice that we now have the three medians intersecting at one point and 1/3 the distance for each. Thus, we can construct a construct a triangle around them.
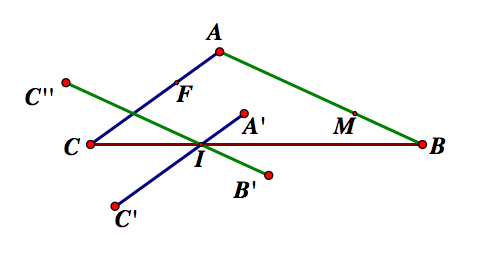
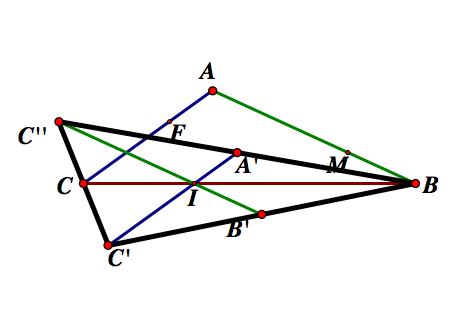
All that's left is to check that the medians are actually at the midpoints of the sides of the triangle. We can also check out construction to see that as the median lengths change, so does the triangle.