In this assignment, we will investigate tangent circles. There are three possible cases to consider.
Case 1 - When the two circles are disjoint.
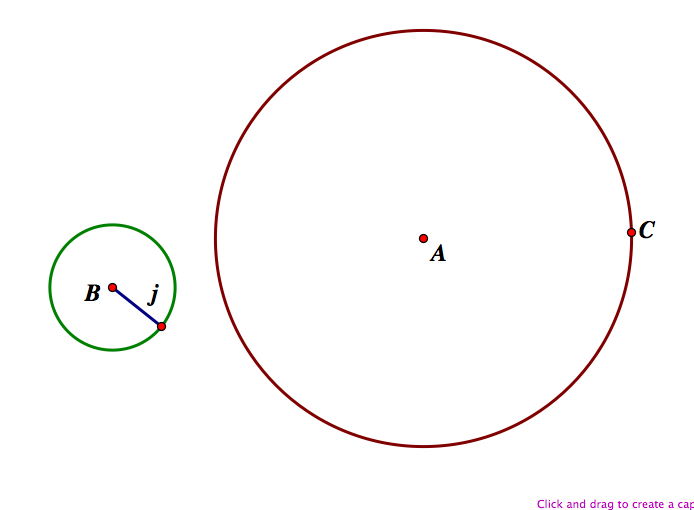
We will let the point C be the point of tangency on circle A. Next, we will construct a line through points A and C. Then construct a circle with center C and radius j. This circle intersects line AC at a point, which we call F. (NOTE: Circle with center C intersects AC in two locations, but we will choose the point that lies outside of circle A for now). We will come back to the inner point later.
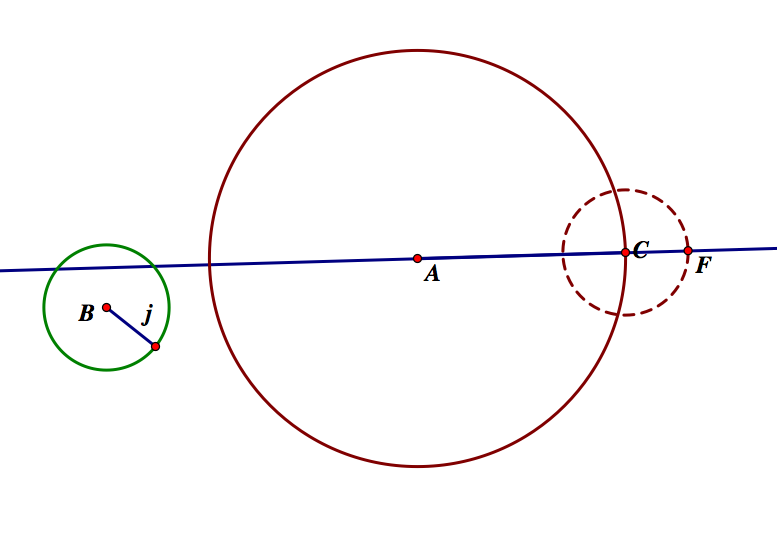
Now, we will construct segment BF. Then, we will construct the perpendicular bisector to BF (through the midpoint, we will call G). This line will intersect AC at a point, we'll call H.
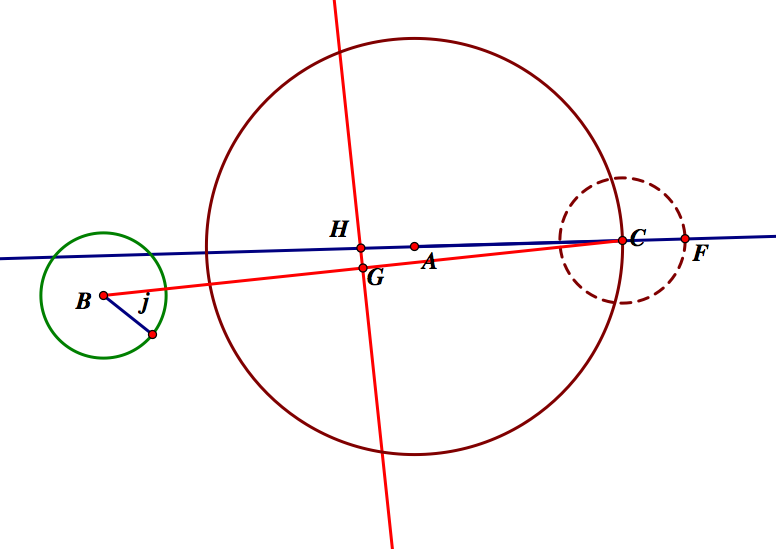
From what we know about perpendicular bisectors, segments FH and BH are congruent. We also know that segments CF and BD are congruent, by construction since they are radii of congruent circles. Thus FH - CH = BH - BD, or HC = HD.
From this, we can construct a circle with center H, with radius HC=HD. This circle, in light blue, will be tangent to circle A, at C, and B, at the new point D.
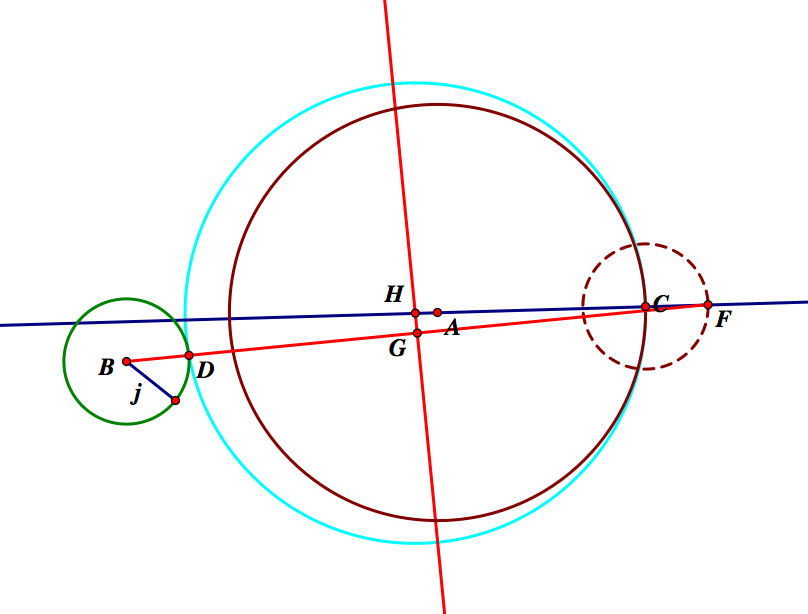
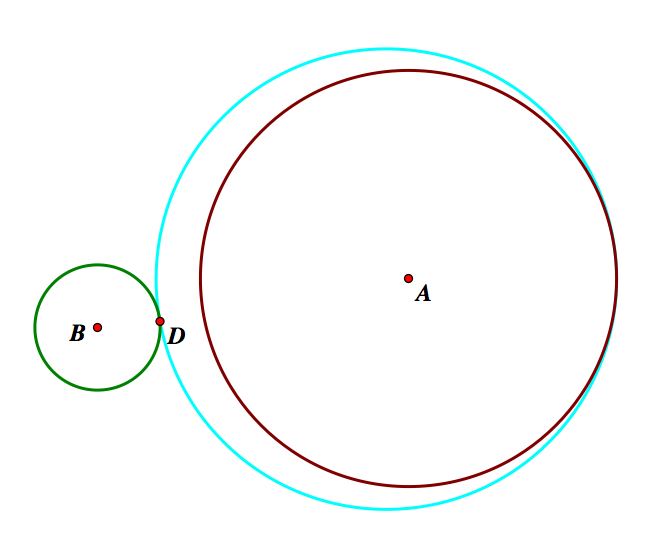
Hiding our constructions, we can better see out tangent circle.
Remember the other intersection point of the circle C and the line AC? Well, now we will do the construction using this point. Let's call it E.
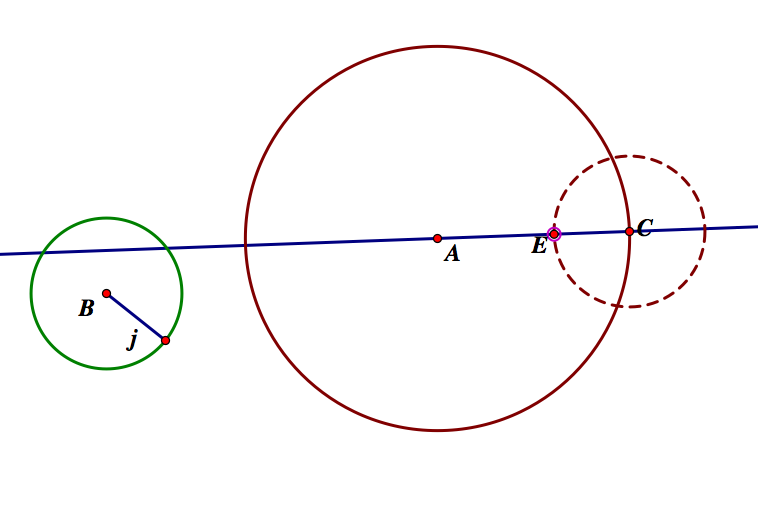
Next, we will follow the same construction as above, but with point E.
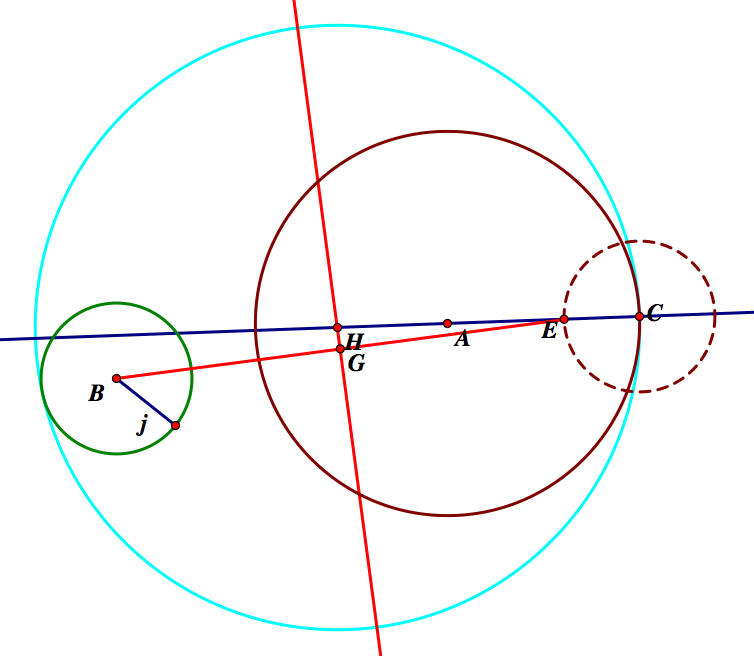
Hiding our constructions, we can better see our tangent circles.
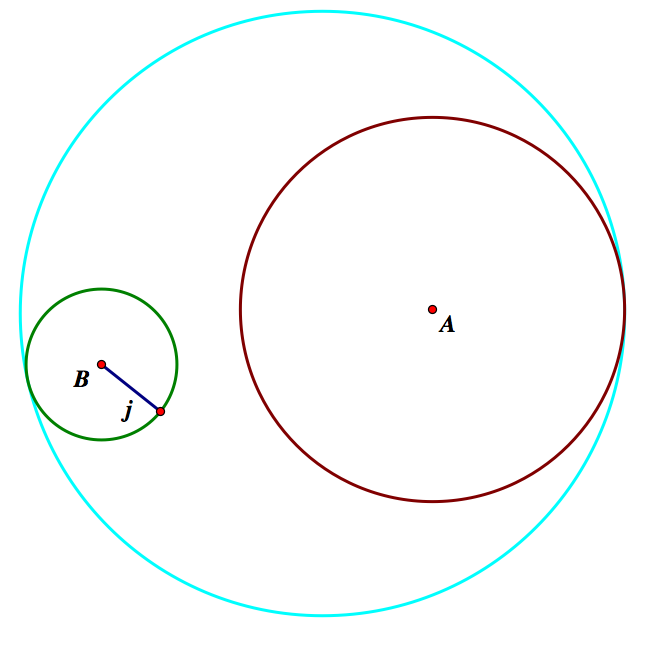
This concludes Case 1. Now we will examine Case 2- when the two circles intersect.
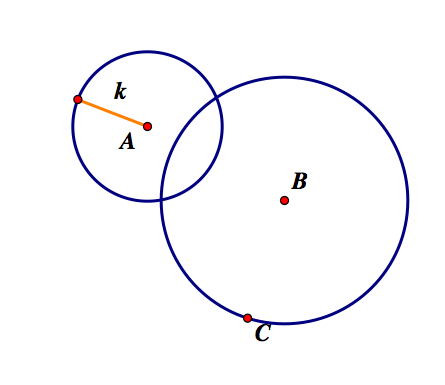
This construction follows the same as above. Here is the resulting tangent circle, with our construction and without.
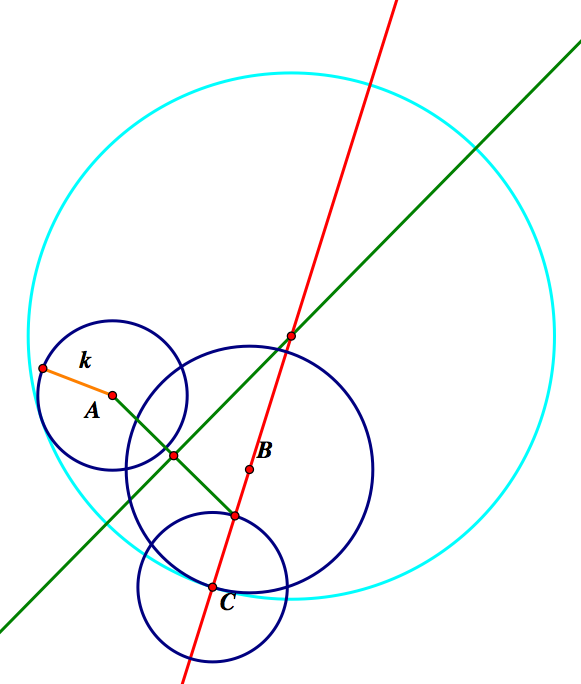
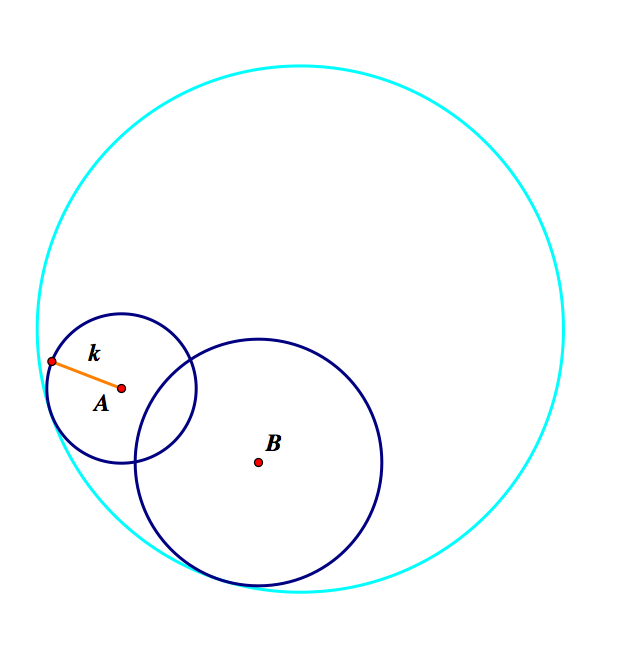
Again, we have another case, using the intersection point of C and CB outside of B. Here is the resulting tangent circle, with and without our constructions.
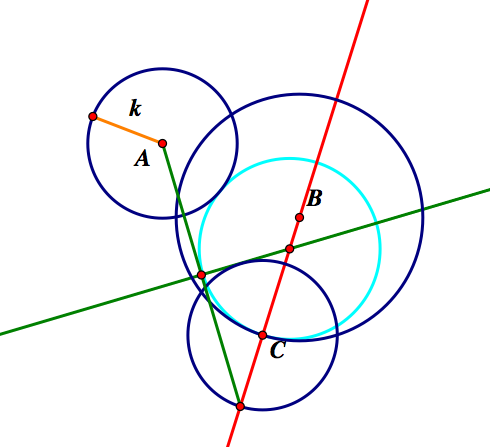
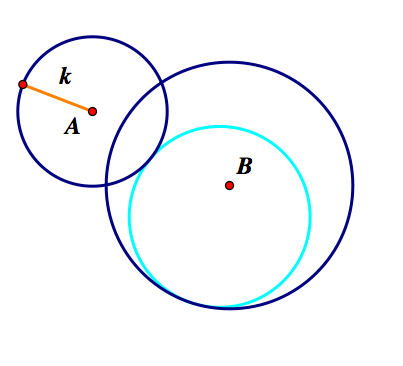
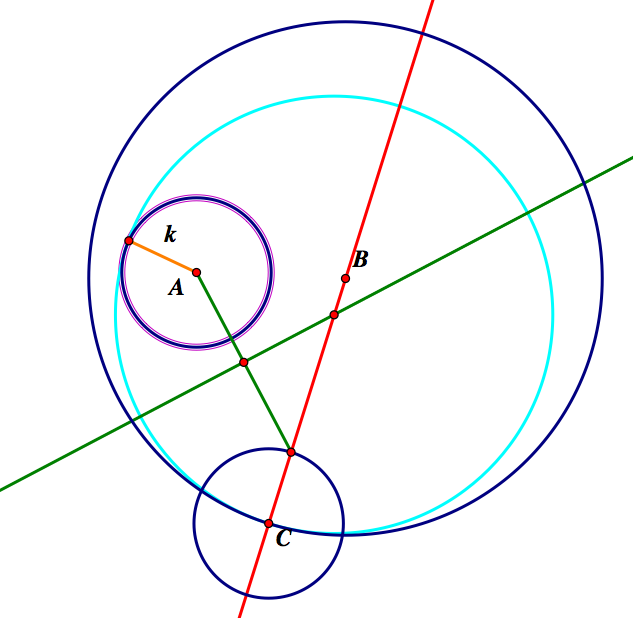
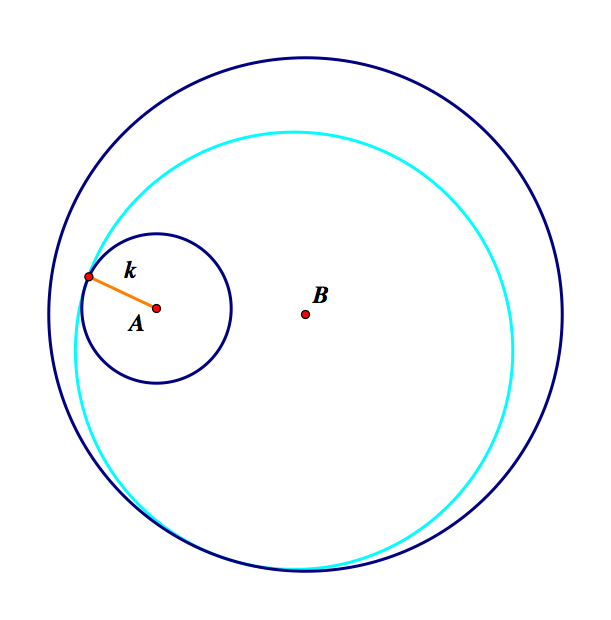
Finally, we have Case 3- where one circle is inside the other.
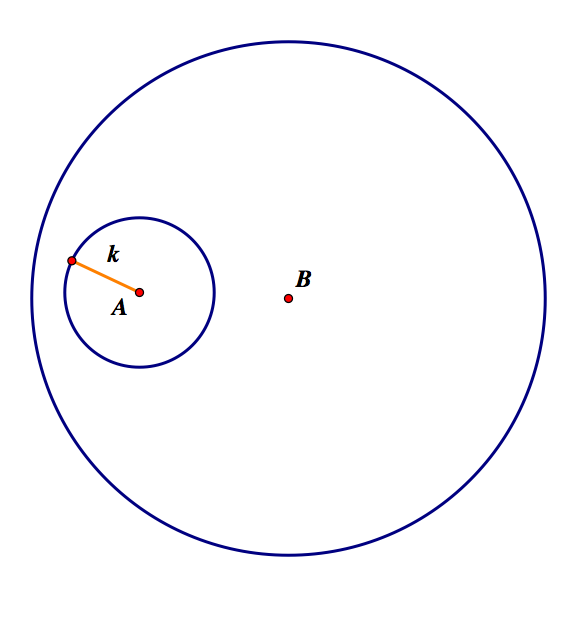
This construction also follows from the one above. We, again, have two cases. Let's examine the case of the outside intersection of C and BC. Below it is shown with and without the construction.
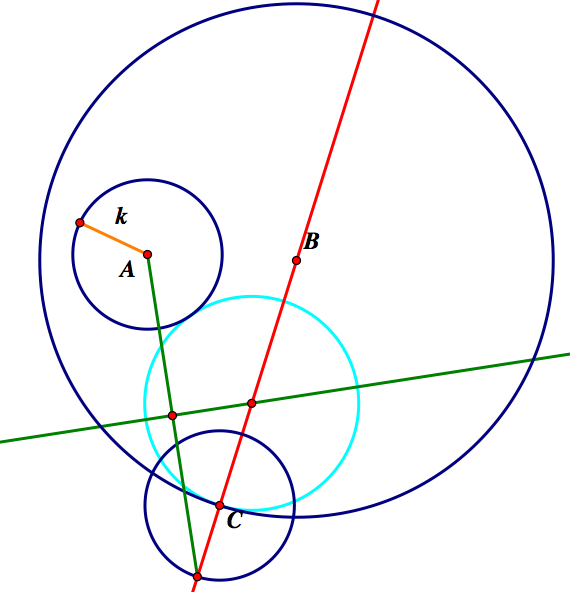
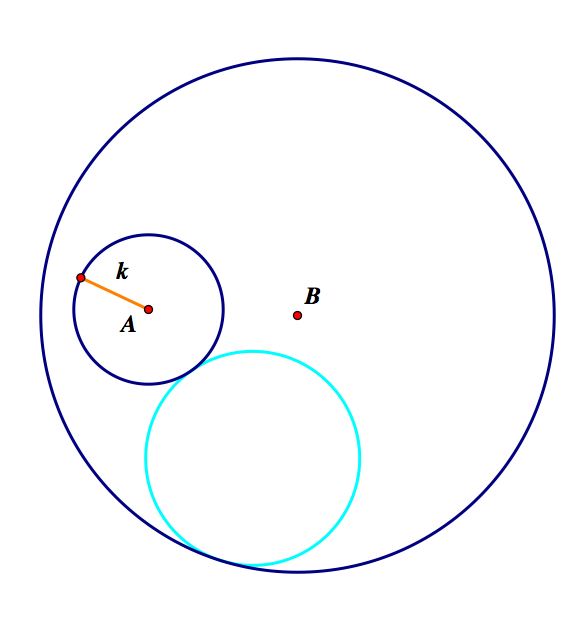
Our last case is the case using the inside intersection of C and CB. Below the tangent circle is shown with constructions and without construction.