

by: Bennett Lewis
Let's consider the triangle ABC. We will be doing investigations with altitudes and orthocenters.
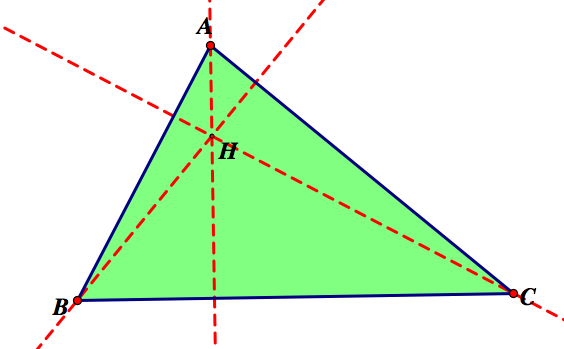
So the orthocenter of ABC is shown below, by point H.
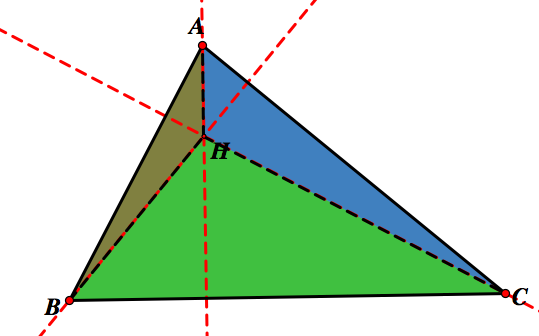
Notice that this creates three smaller triangles: ABH, ACH, and BCH. They are represented in the image below. The black lines show the boundaries of the triangles.
Now, we will find the orthocenter of each of the smaller triangles.
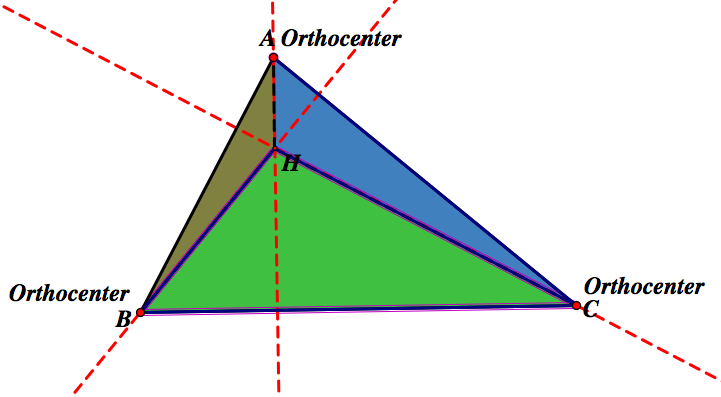
The three orthocenters of the smaller triangles are the vertices of the triangle ABC. How is this possible?
Let's recall the definition of orthocenter. The orthocenter of a triangle is the point where all three altitudes of a triangle meet. Also to refresh our memory, an altitude is a line which passes through a vertex of a triangle, and is at right angles to the opposite side. Notice that the for the triangle BHC, the altitude for vertex H is the altitude for A, the altitude for B and C are the BH and CH respectively, from our previous investigation. Then the only point where those three lines meet is at vertex A. A similar argument shows that vertex C is the orthocenter for ABH, and vertex B is the orthocenter for AHC.
Now, we will construct the circumcircles for all 4 triangles.
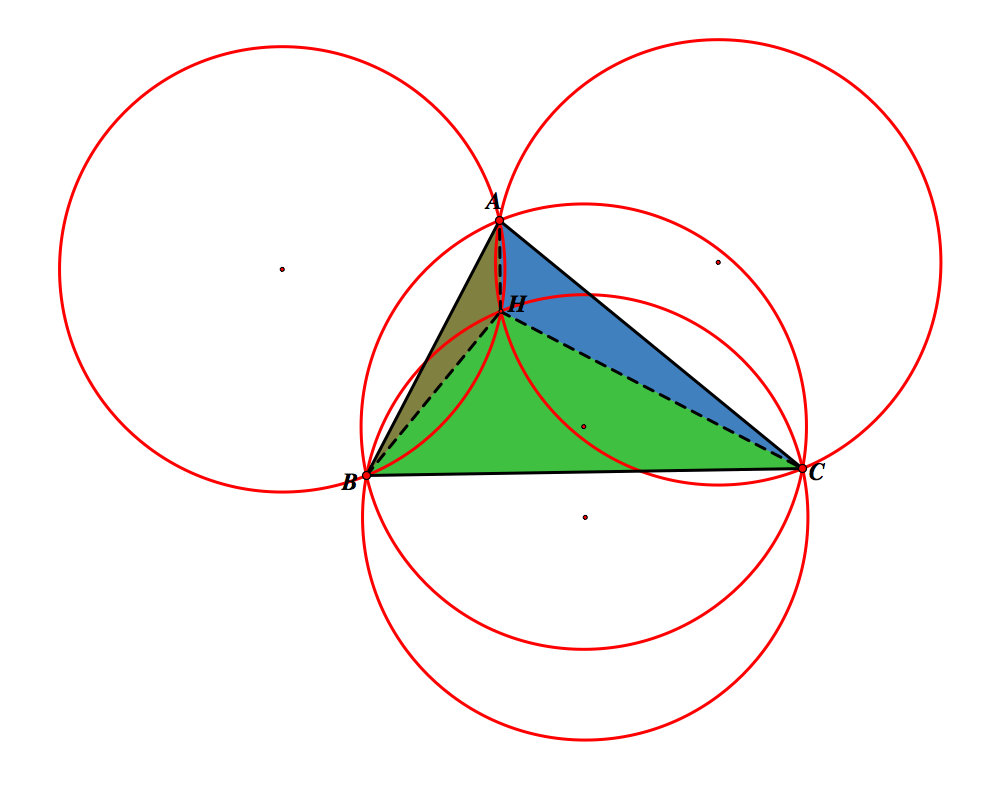
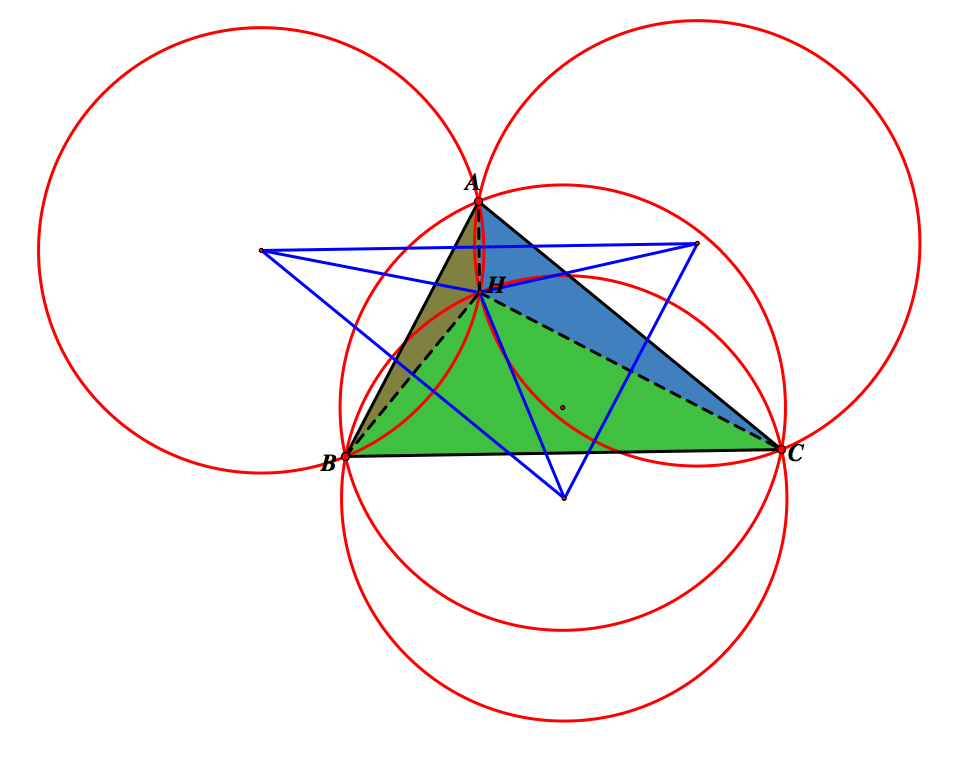
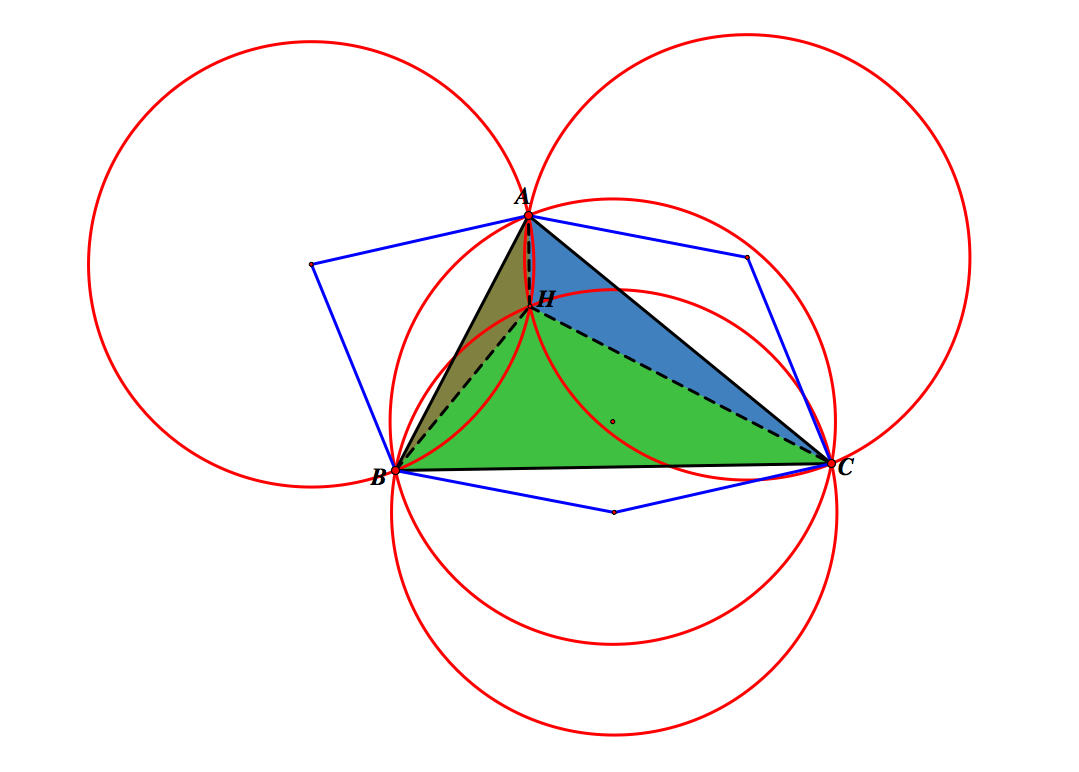
Notice from the images above the circumcircles of the subtriangles are congruent to the subtriangles of the original triangle ABC. Also notice that all 4 circumcircles are congruent. If we connect the centers of the 3 circumcircles of the subtriangles and the vertices of the original triangle, we obtain a 6-sided polygon, or hexagon.
What happens if the original vertices are dragged to where the orthocenter is? Let's take a look. Let's move A to H.
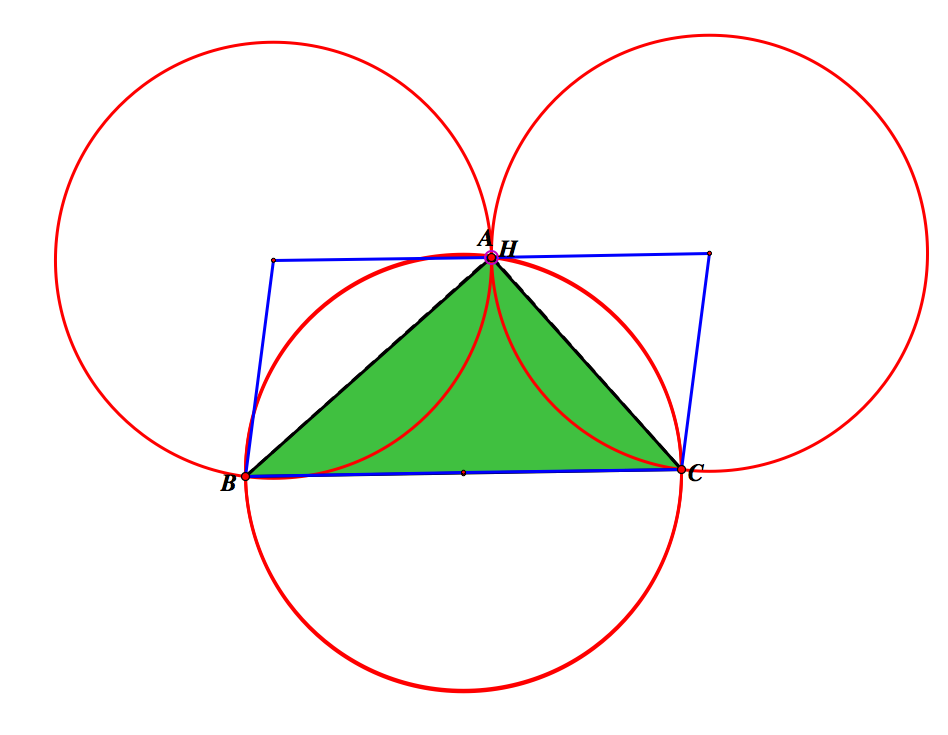
Notice that instead of a hexagon, we get a parallelogram. Here the short sides are congruent to the radii of the circumcircles. The long sides are congruent to the diameter of the circumcircles.
Check out this link here for the GSP file to see what happens when the vertices are moved to different locations.
Now we will take a look at the nine point circles of each triangle. Where do you think they will be?
Let's recall what the nine point circle:
1) midpoints of the sides of the triangle
2) the feet of the altitudes of the triangle
3) the three midpoints of the altitude segments in between the orthocenter and the respective vertices.
Below is the nine point circle for our original triangle ABC.
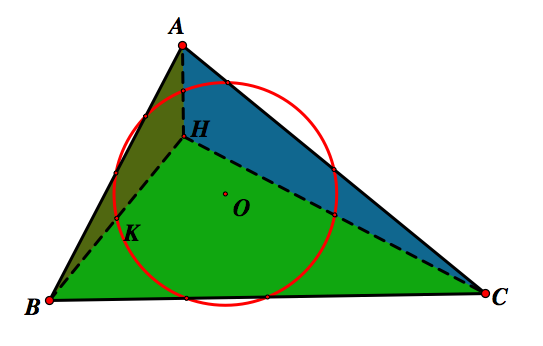
Now let's look at the nine point circles for the subtriangles.


Above is the nine point circle for ABH. Above right is the nine point circle of ACH. Any guesses on where the nine point circle for BCH will be?
I bet you got it, it's the same!

As we observed, the triangles share the same nine point circle. This conclusion correlates to our earlier conclusion that the triangles have the same orthocenter. What other conclusions can we draw? Check out the GSP file here to do some more investigations with the nine point circle.