---

Assignment 9:

Pedal Triangles

By Bennett Lewis

---

Given a point and a triangle, the pedal triangle is the triangle whose vertices are the feet of the perpendiculars from the point to the sides of the given triangle.

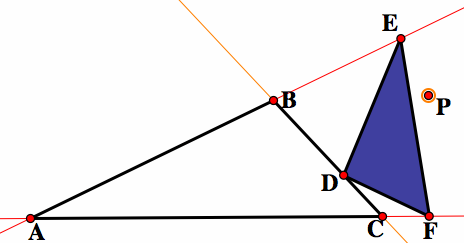
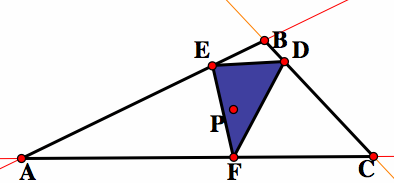
In the picture above, our original triangle is ABC and our point is P. Thus, the pedal triangle is DEF. The points D, E, and F are the points of intersections between the lines of the triangle ABC and the perpendicular lines to the lines of the triangle through P. The pedal point may lie within, outside, or on the given triangle. Below left shows the pedal point inside the original triangle. Below right shows the pedal point on one of the side of the original triangle. Notice that when the pedal point, P, is on the side of the triangle, it is also the vertex of the pedal triangle.

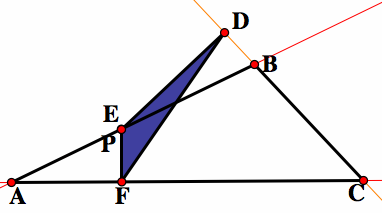
When the vertices of the pedal triangle are collinear such that the triangle is degenerate, the line created from them is called the Simson Line. Below is the picture of the original triangle and the Simson line.

Now, let’s explore a special case and its properties. First, let’s draw the circumcircle of ABC with center W. Now we’ll construct another circle centered at W, but this one will be slightly larger than the circumcircle, and the pedal point P will be contained on this circle. Also, we will construct the midpoints of the pedal triangle.Now we will examine the locus of points made by the midpoints of the pedal triangle.

 

When we trace these points, allowing the pedal point to travel around the larger circle, the midpoints of the pedal triangle create ellipses. Use the this script tool hereto explore more.

---