
Part 3:
Field goal Investigations
By Bennett Lewis
The football rules in college football were changed a few years ago have made the uprights 5 feet narrower than previously. Many game commentators have harped about how much harder it is to kick field goals from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does the kicker have maximum angle to the two uprights.
Some Important Information:
Length of a football field: 120 yds
Width of a football field: 53 1/3 yds
Width of Hash Marks: 13 1/3 yds
Width of Goal Posts: 6 1/5 yds
Now we will construct a field using these proportions. You can see the Geometer's Sketchpad (GSP) link here.
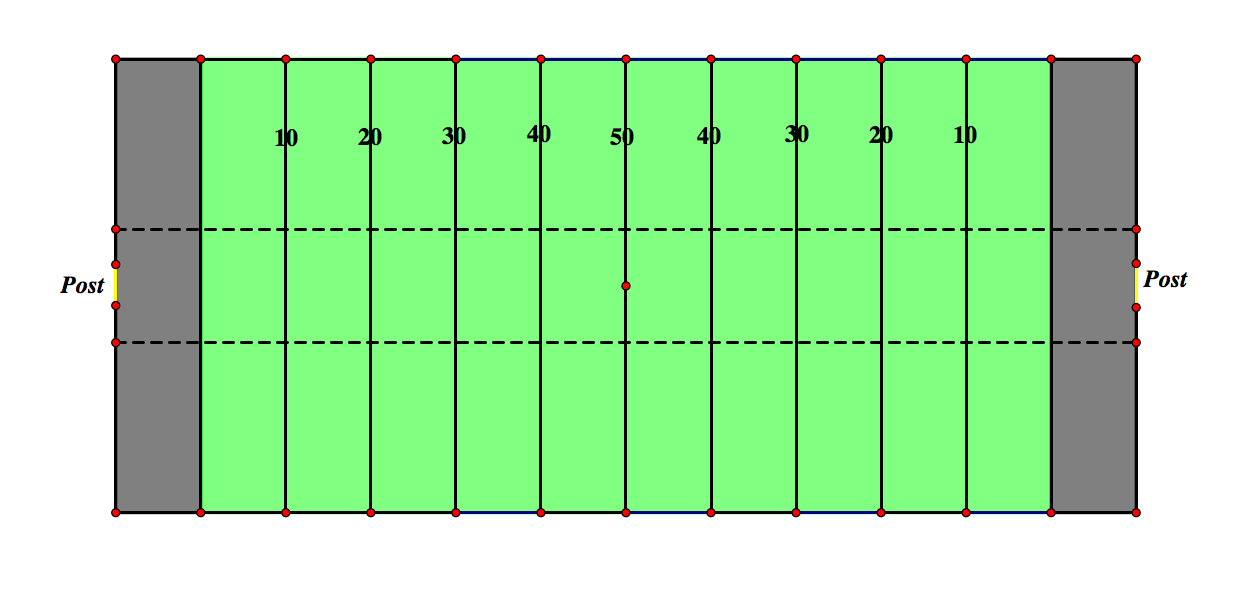
Using the sketch from GSP, we can create the situation of kicking from the hash mark. Click the image below to open this GSP file.

You will notice in this GPS file, that the angle measure is shown and that the distance from the kicker to the goal post is also shown in centimeters. Using some simple calculations, we can convert that measure into yards.
Giving us this formula 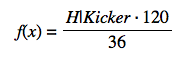 . As we drag along the hash mark, you will see the function calculate the distance in yards.
. As we drag along the hash mark, you will see the function calculate the distance in yards.
You will also see the angle measure of the red highlighted triangle. This will allow us to compare the angle between same yardage field goals from the hash mark and the center of the field.
Now, we will create the triangle from the center of the field and compare those results. Click the picture below to see the GSP file.
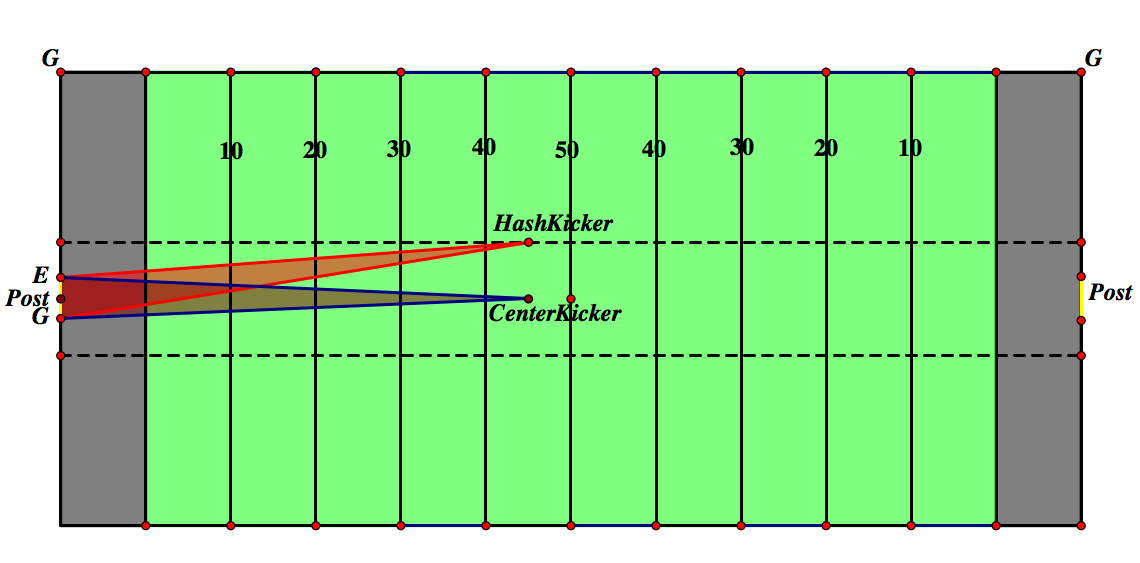
You will notice above the field, the measurement for distance in yards and the angles for each kicker.
Using these formulas, a if the kicker kicks from the Shamrock 55 yds away, the angle is about 4.95 degrees.
If the kicker is 55 yds away in the center of the field, then the angle is about 5.02 degrees.
So, we can see that changing the position from the hash mark to the center of the field does not give enough difference to matter. The kick from the middle of the field gives a slightly better angle, but not a significant one.



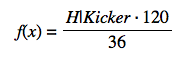 . As we drag along the hash mark, you will see the function calculate the distance in yards.
. As we drag along the hash mark, you will see the function calculate the distance in yards. 