
Part 2:
Square Inscribed in a Circle
By Bennett Lewis
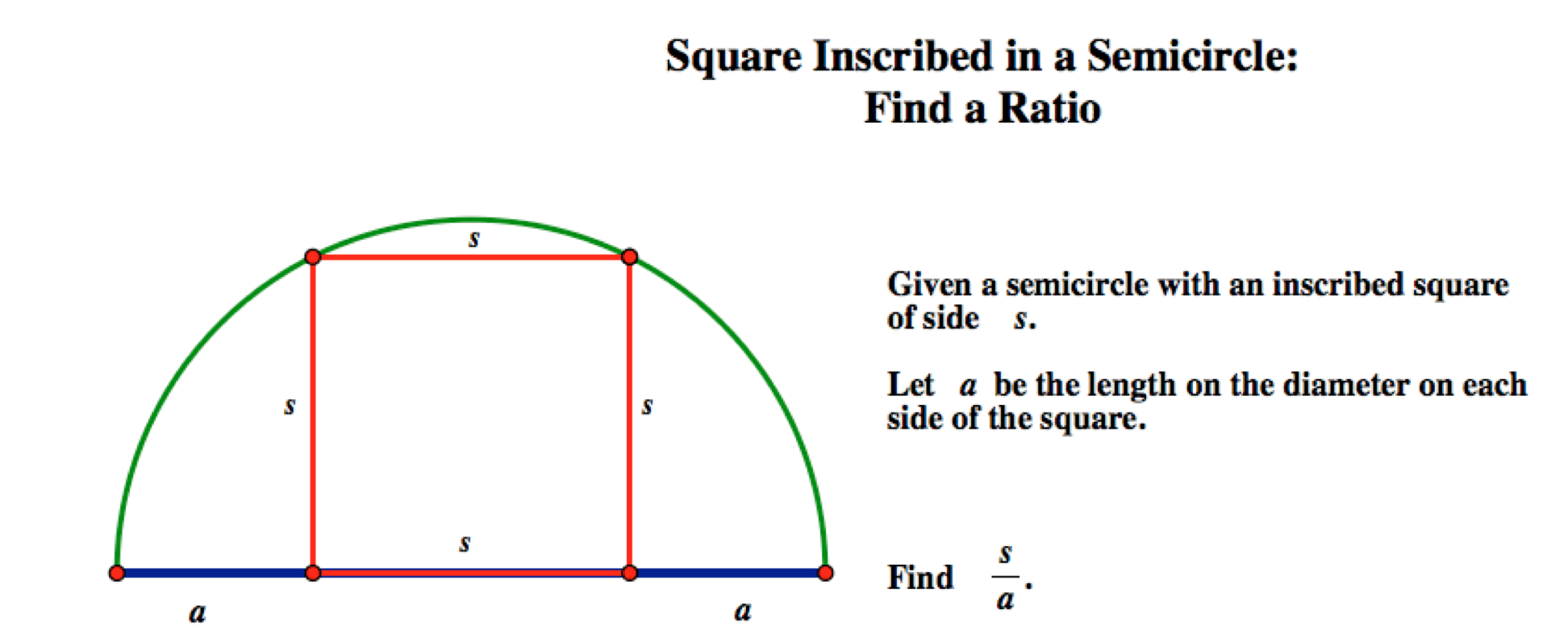
We can construct this figure in Geometer's Sketchpad. Check out a file for it here.
We can see that the midpoint of the side of the square along the diameter is also the midpoint of the diameter. Therefore, we know that the distance from the midpoint to one of the opposite corners of the square is a radius of the semicircle.
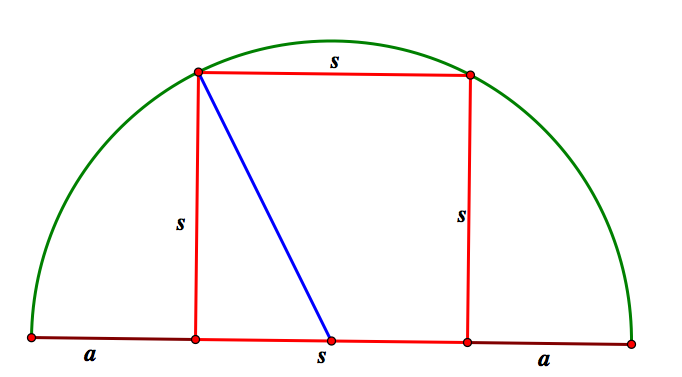
The triangle formed here, is a right triangle, since the base angle is also an angle of the square. Then we can use Pythagorean Theorem to find r.
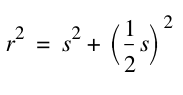
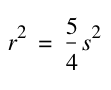
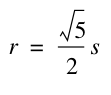
We also know that
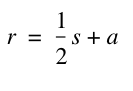
Therefore we can set these two equations equal to each other. This will allow us to solve for ![]() .
.
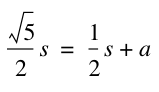
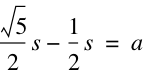
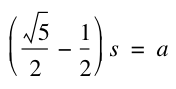
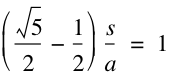
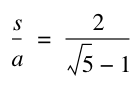
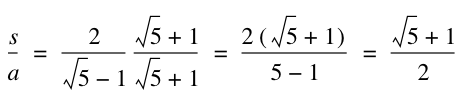
This is the Golden Ratio!