by: Doris Santarone
Assignment #12: Fibonnaci Sequence
The Fibonnaci sequence is a recursive sequence named after Leionardo Pisano. It is defined as f(n) = f(n-1) + f(n-2), where f(0) = 1 and f(1) = 1. In this assignment, I want to investigate the Fibonnaci sequence.
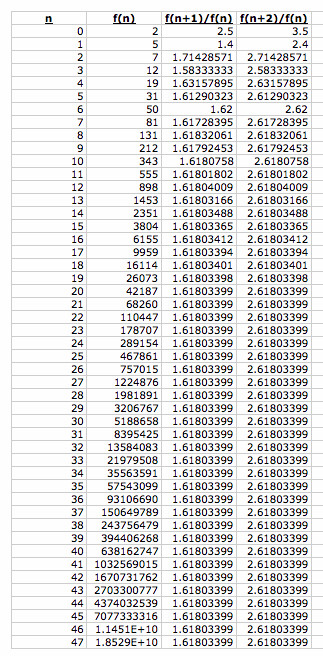
Below, f(n) represents the nth Fibonnaci number.
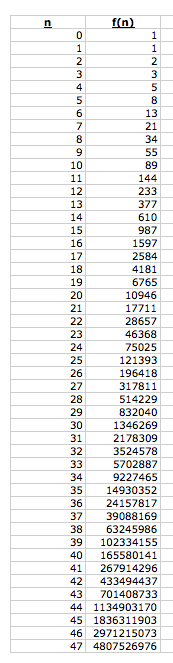
Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence.
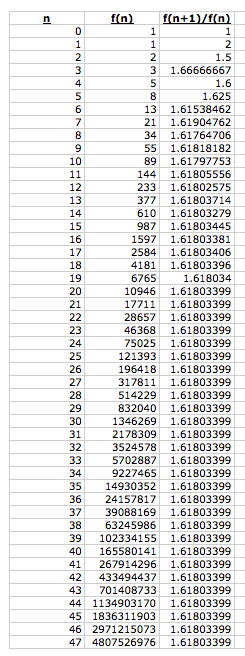
As n gets larger, the ratio of adjacent terms in the Fibonnaci sequence converges toward 1.61803399, or the Golden Mean!! Why does this happen? Let's see if we can prove it...
Let g(n) be the nth number in the sequence of ratios.
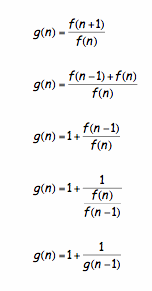
Suppose the sequence converges to a real number g, then 
and 
(g(n) and g(n-1) have the same limit). Thus, the real number g to which the ratio of Fibonnaci numbers converges to must satisfy the following equation: 
. After solving this equation for x, we see that...
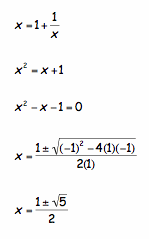
The positive root is 
or 1.61803399...The Golden Mean!!
What if we construct the ratio of every second Fibonnaci number?? Let's see...
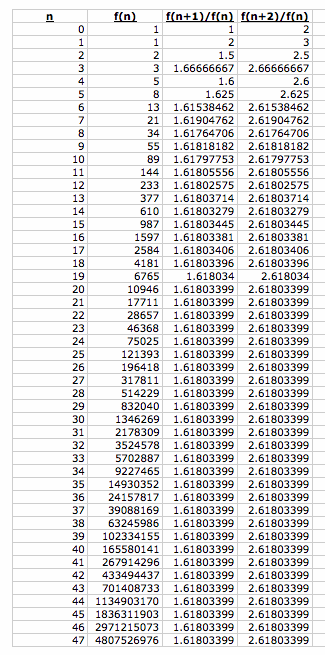
Let h(n) be the ratio of every second Fibonaci number. As n gets larger, h(n) converge to 2.61803399, or 1.61803399+1, the Golden Mean + 1!!
Click HERE for the Excel spreadsheet.
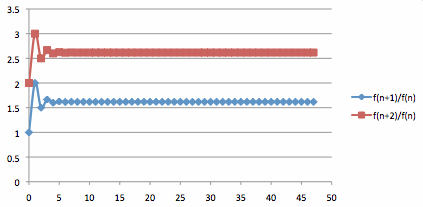
Below is a graph of g(n) and h(n). You can see that g(n) converges to 1.61803399, while h(n) converges to 2.61803399.
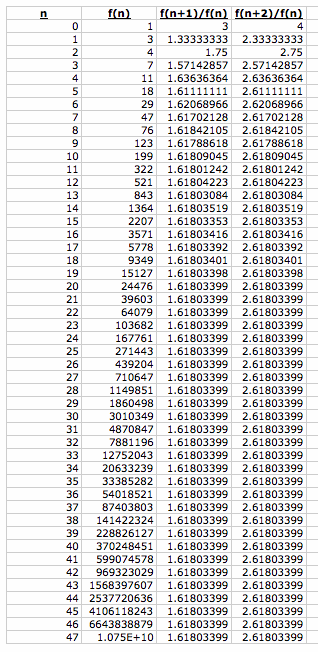
What if we change the first two numbers in the sequence? What if f(0)=1 and f(1) = 3?? See below:
Click HERE for this Excel spreadsheet.
WOW!!! We see the same behavior. As n gets larger, f(n+1)/f(n) converges to the Golden Mean and f(n+2)/f(n) converges to the Golden Mean + 1!!! Does this work for any values of f(0) and f(1)? Here are a few more...
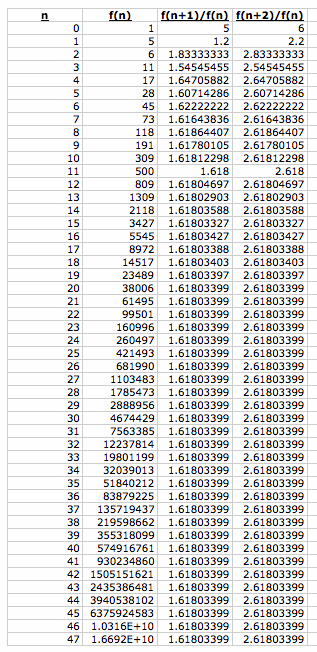
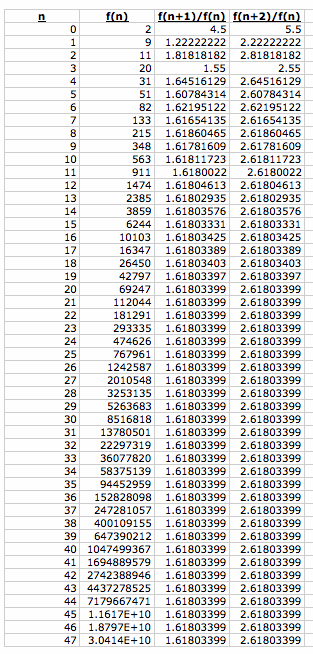
Yes!! The Golden Mean appears no matter what values we choose for f(0) and f(1)!!!