by: Doris Santarone

Assignment #3: Quadratics in the xb Plane

Consider the quadratic: . If we graph this quadratic in the xb plane, we see this:

 

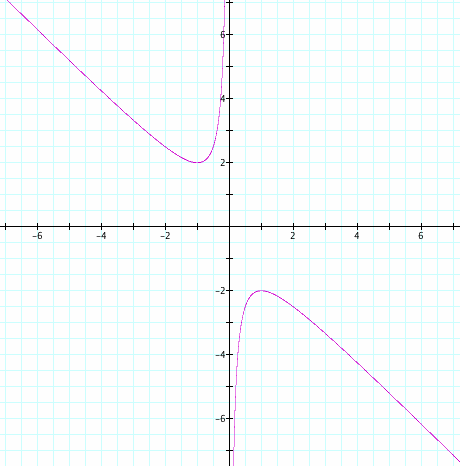
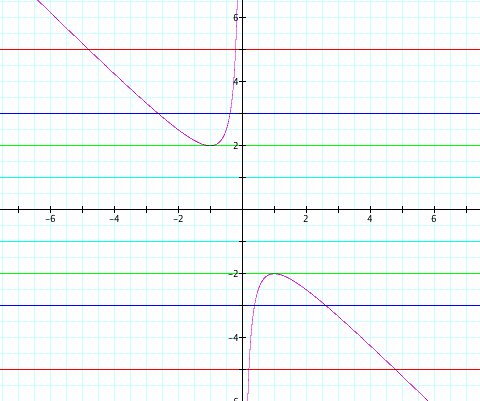
The graph is a hyperbola. This hyperbola has the following characteristics:

1) The equation for the hyperbola in function notation is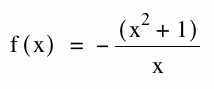

2) Vertical asymptote at x = 0

3) Oblique asymptote at y = -x (can find this by calculating the division through long division of synthetic division)

4) The graph has a local minimum at (-1, 2) and a local maximum at (1, -2).

5) The domain of the hyperbola is (-infinity, 0) (0, infinity).

6) The range of the hyperbola is (-infinity,-2) (2, infinity)

 

 

See the graph here that contains the asymptotes and the local minimum and local maximum.

 

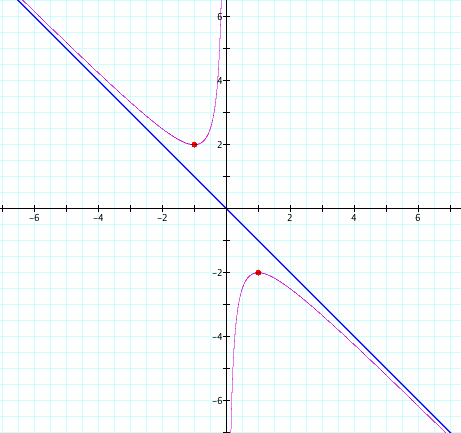
If you take a particular value of b, such as 4, and graph this on the same graph as the hyperbola, we will see this:

 

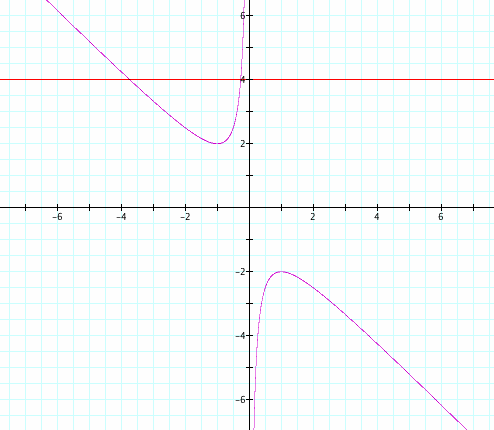
The line b = 4 is a horizontal line that intersects the hyperbola at two points. These two points tell us the roots of the original quadratic , where b = 4. Let's graph several values of b, say b = -5, -3, -2, -1, 1, 2, 3, and 5.

 

For any b value, where b < -2 or b > 2, there are 2 roots. For b = -1 and b = 1, there is only one root. And for -2 < b < 2, there are no roots.

 

 

Now, consider the quadratic: . When we graph this quadratic in the xb plane, we see this:

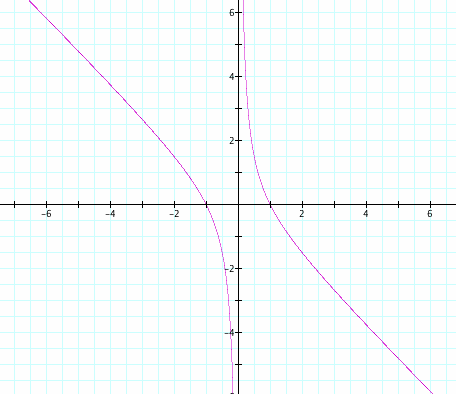
If we graph some values of b, say b = -5, -3, -2, -1, 1, 2, 3, and 5 on the same graph, we get:

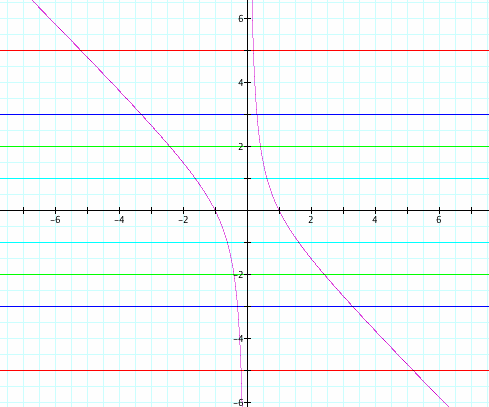
You can see that for the quadratic , there are always 2 roots. So, when does this change? For what values of c does the quadratic always have 2 roots and when does it not? View the animation below for c values in the interval (-10,10).

When c < 0, the quadratic always has 2 roots!

---

Back to Homepage

---