by: Doris Santarone

A Library of GSP Scripts

Instead of recreating a construction over and over again, we can make our lives a little easier using the GSP scripts feature. They are an efficient way of repeating constructions. Below is a library of GSP scripts. For each construction, I have listed the necessary givens. I have also linked to the GSP sketch, where you can use the script.

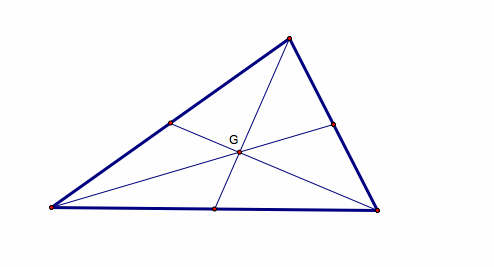
1. Centroid – the centroid, G, of a triangle is the common intersection of the medians of a triangle.

Given: Points A, B, and C (vertices of triangle)

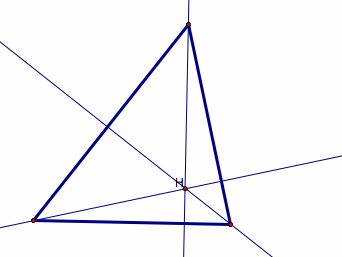
2. Orthocenter – the orthocenter, H, of a triangle is the point of concurrency or the common intersection of the three lines containing the altitudes.

Given: Points A, B, and C (vertices of triangle)

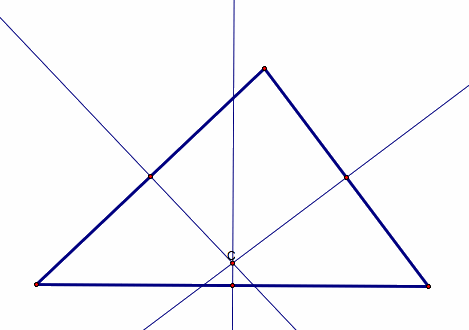
3. Circumcenter – the circumcenter, C, of a triangle is the point in the plane equidistant from the three vertices of the triangle.

Given: Points A, B, and C (vertices of triangle)

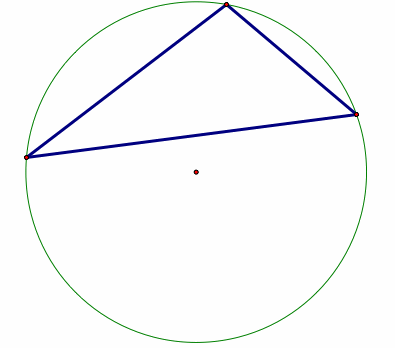
4. Circumcircle – a circle where the center is C, circumcenter and where the 3 vertices of the triangle lie on the circle.

Given: Points A, B, and C (vertices of triangle)

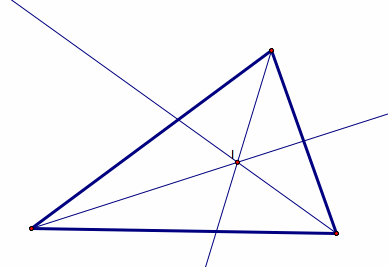
5. Incenter – the incenter, I, of a triangle is the point on the interior of the triangle that is equidistant from the three sides.

Given: Points A, B, and C (vertices of triangle)

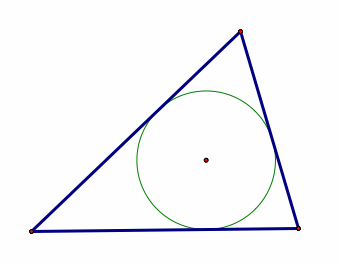
6. Incircle - a circle where the center is I, incenter and where the 3 feet of the altitudes of the triangle lie on the circle.

Given: Points A, B, and C (vertices of triangle)

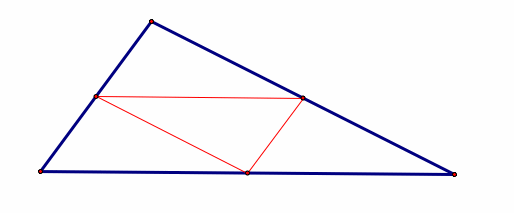
7. Medial triangle – the triangle formed by connecting the mid-points of each side of the triangle.

Given: Points A, B, and C (vertices of triangle)

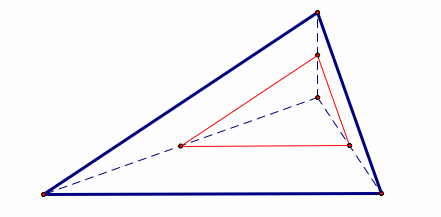
8. Orthocenter, Mid-segment triangle – the triangle formed by connecting the mid-points of the segments from the orthocenter to the vertices.

Given: Points A, B, and C (vertices of triangle)

9. Orthic triangle – the triangle formed by connecting the feet of the altitudes of a triangle.

Given: Points A, B, and C (vertices of triangle)

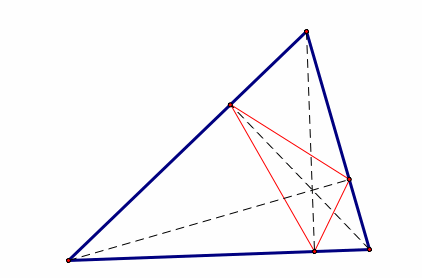
10. Pedal triangle – Given a triangle ABC and any point E in the plane, this is the triangle formed by the perpendiculars to the sides of ABC.

Given: Points A, B, and C (vertices of triangle)

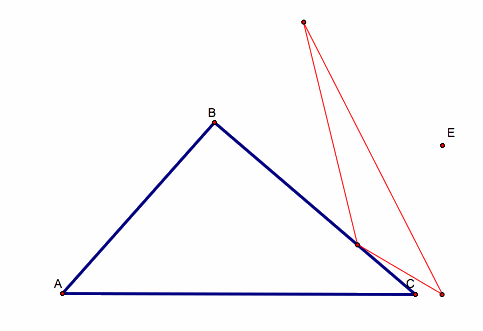
11. Center of Nine point circle – the center of any Nine point circle lies on the corresponding triangle's Euler's line, at the midpoint between that triangle's orthocenter and circumcenter.

Given: Points A, B, and C (vertices of triangle)

12. Nine Point Circle - a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle. These nine points are: the midpoint of each side of the triangle , the foot of eacha altitude, the midpoint of the line segment from each vertex of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes).

Given: Points A, B, and C (vertices of triangle)

13. Trisecting a line segment

Given: Points A and B (to form segment AB)

14. Equilateral triangle, given a side

Given: Points A and B (to form one side of the equilateral triangle)

15. Square, given a side

Given: Points A and B (to form one side of the square)

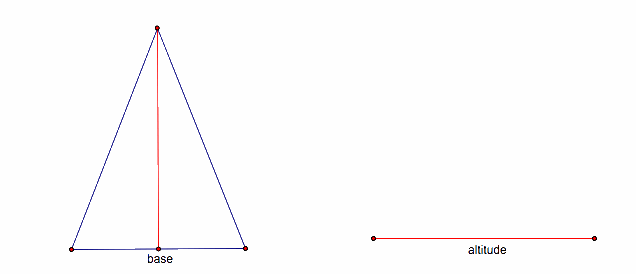
16. Isosceles triangle, given base and altitude

Given: Points A, B, C, and D (Segment AB will be the base, and segment CD will be the altitude)

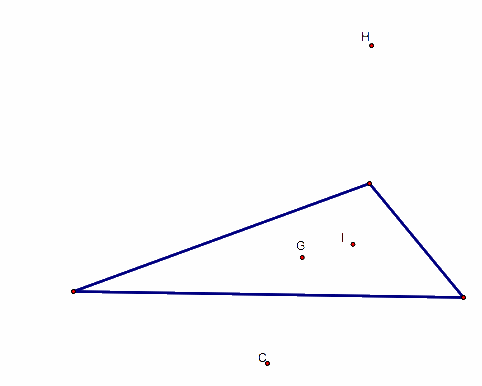
17. Triangle Centers (H, G, C, and I)

Given: Points A, B, and C (vertices of triangle)

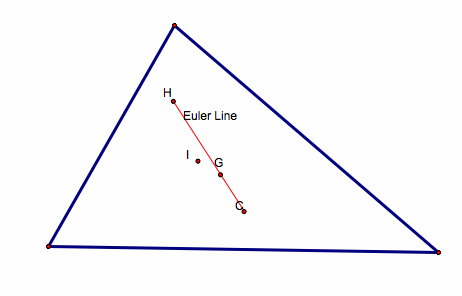
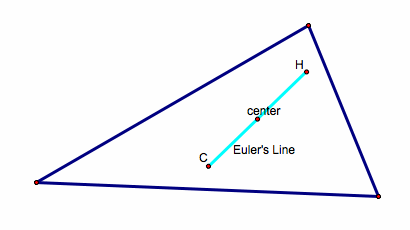
18. Triangle Centers with Euler Line

Given: Points A, B, and C (vertices of triangle)

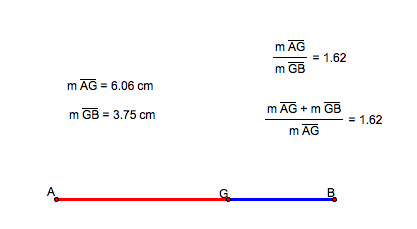
19. Divide a segment AB into two parts that form a golden ratio

Given: Points A and B (to form segment AB)

20. Pentagon, given a radius

Given: Points A and B (to form radius of the pentagon)

21. Pentagon, given a side

Given: Points A and B (to form one side of the pentagon)

22. Hexagon, given a radius

Given: Points A and B (to form radius of the hexagon)

23. Hexagon, given a side

Given: Points A and B (to form one side of the hexagon)

24. Octagon, given a radius

Given: Points A and B (to form radius of the octagon)

25. Octagon, given a side

Given: Points A and B (to form one side of the octagon)

26. Triangle, given its medians

Given: Points A and B (to form one median), points C and D (to form a 2nd median), and points E and F (to form a 3rd median).

27. Circle tangent to 2 other Circles

Given: Points A and B (to form circle AB) and points C and D (to form circle CD)

There are 2 constructions to find a circle tangent to circles AB and CD. Below are the 2 options and their respective links.

Click here for the GSP Sketch (including the script).

Click here for this GSP Sketch (and the script).

---

Back to Homepage

---