by: Doris Santarone
Proof of Napolean's Triangle using Similarity
Just like our previous proof, we will start with this original sketch (with the equilateral triangles constructed outward).
Fix N as a center of rotation, and rotate the entire figure by 120 degrees. You can see that triangle ABZ maps to itself, along with its center N. All the other points can be found below, notated where point X maps to X', Y to Y', etc.
Connect X' to Y and L' to M, as shown below:
Because of the rigidity of the rotation, triangle LMN is congruent to triangle L'M'N. In particular, ML to congruent to M'L'.
Next, let's look at point A. There are six triangles that include point A as a vertex. We want to concentrate on the three equilateral triangles, triangle AX'C', triangle ABZ, and triangle ACY. Since these 3 triangles are equilateral triangles, then each of their angles is equal to 60 degrees.
Using the fact that the angles around point A sum to 360 degrees and the fact above, we can say that
Now, we know that angle ZAC' is congruent to angle ABC from the rigid rotation. Thus,
Since the three angles of a triangle sum to 180 degrees, we know 
. From substitution, we know that
. This leads us to see that 
.
Now look at pentagon CYX'C'A and pentagon YABXC.
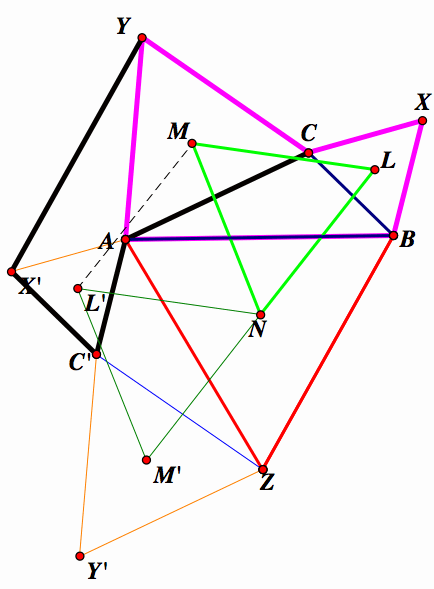
Since triangle AX'C' is the rotation result of BXC, then AC' is congruent to BC and X'C' is congruent to XC. Since triangle AYC is equilateral, then YC is congruent to AC and AY is congruent to YC. Finally, because triangle ABC is congruent to triangle YX'A (from above), then X'Y is congruent to BA. All of these things lead us to say that pentagon CYX'C'A is congruent to pentagon YABXC. It follows that ML' is congruent to ML. Since M'L' was constructed from the rigid rotation of ML, then M'L' is congruent to ML. Finally, we can say ML = ML' = M'L'.
Next, we rotate original figure by -120 degrees to obtain the figure below:
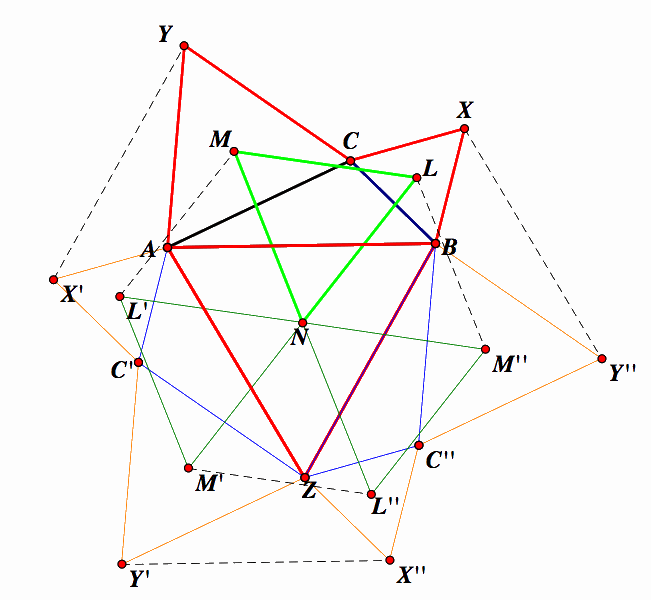
With the same reasoning as before, we can say that pentagon C''Y''XCB is also congruent to pentagon YABXC, which means ML = M''L. Also, pentagon Y''BZX''C'' is congruent to pentagon YABXC, which means M''L'' =ML. Finally, pentagon C''Y''X''C''Z is congruent to pentagon YABXC, which means M'L'' is congruent to ML.
All of this leads us to see that ML = ML' = M'L' = M'L'' = M'L'' = M''L'', forming a hexagon. From the rigid rotation, the angles that meet at N are all 60 degrees, meaning that the hexagon is a regular hexagon. If MLM''L''M'L' is a regular hexagon, then it is made up of 6 equilateral triangles, meaning that triangle MLN is equilateral!!