by: Doris Santarone
Properties of the Triangle ABC,
where the segment DE is parallel to the base BC and divides the area in half.
Assume the area of triangle ABC with base BC is divided in half by segment DE, which is parallel to BC.
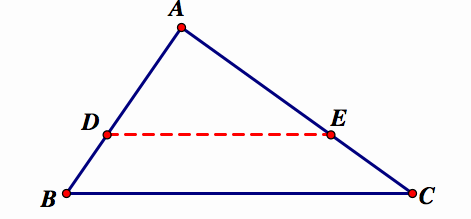
First, I will construct the height of the triangles:
Consider the 2 triangles ADE and ABC. Since DE is parallel to BC, then 
because they are corresponding angles. Angles DAE and BAC are the same angle, so
. Thus, the triangles ADE and ABC are similar. Since the are similar, then the ratio of their corresponding parts are congruent. Thus,
. (eq. 1)
Assuming the area of the triangle was divided in half, 
, or 
. (eq. 2)
Using this equation (2), and substituting with equation (1), we get:
Thus, the ratio of all sides of the triangle ADE to ABC is 
.