When A Circle Meets A Line
Investigating
By Ryan Shannon
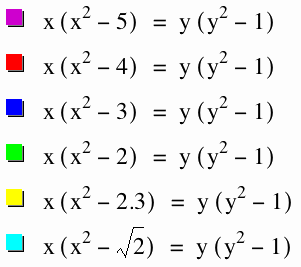
Looking at
where {1<x<6}
The further that n goes from zero we notice that the graph extends (potential place a video here) We talk about how the graph is showing a basic third degree polynomial where there are three roots. Letting x=0 will give us the roots to y, and noticing that the right side is the same we will always have the roots for y=(-1,0,1). This is why the graph will only pass the points {1,0,-1} Also that the x-intercept by letting y=0 we get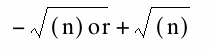 
which is displayed above.
Also from the graph we see a relative shape to a cubic, which is increase, decrease, increase. Noticing that the graph is reflected over the y=x, and too y=x seems to be an asymptote.
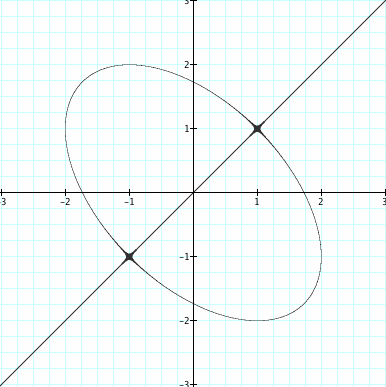
Looking at 
When we decided to place the same value in for the difference of x and y. We are graphing a circle and a straight line, in one phrase. This is actually because the phrase is two graphs. An ellipses and a straight line. thus showing us our asymptote from above.
With the use of some algebraic work we can conclude that is actually 
from this equation we can see that it there are really two graphs molded together, to create this oval and line picture shown below. Then we have
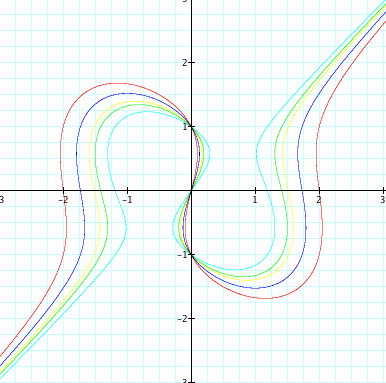
Looking atwhere {-6<x<-1}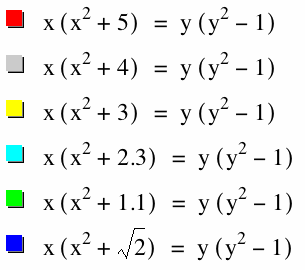
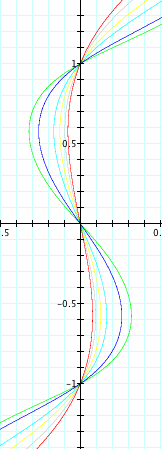
When we change the graph to have a sum on the left and a difference on the right, However when placing the same value for the difference from y and sum from x, we maintain the same graph shape. I see that the graph is passed at {1,0,-1} again. The graph looks to have been a reflection about the origin.
Noticing that the graph is no longer a function, and seeing that the graph only passes (0,0) for and x-value, makes me believe there are no real roots.