a

 

Second Degree Equations

Ronald Aguilar

 

 

Here we investigate the equation and we are looking at the variable a which is the coefficient. First, lets graph the basic equation for a parabola, w.

x

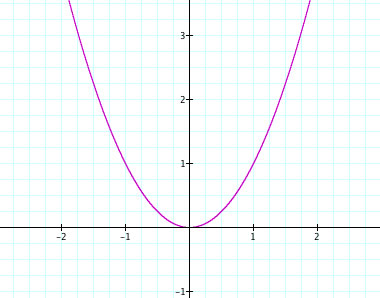
Notice how the graph looks like a U. Now that we have seen the graph for w, lets see what happens when we make 0 < a < 1 and a < 1. Here we use o (graph in blue) and   t  (in red).

t

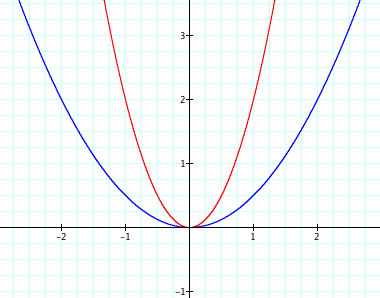
Notice how the graph  of  o gets wider as compared to w.    If we plug in 1 for x the outcome of the function is 1/2 (y = 1/2).   Since the function is even if we plug in -1 for x the outcome is the same, 1/2 (y = 1/2). The graph o  grows slower than  w. The graph of  t gets slimmer as compared to w. If we plug in 1 for x the outcome of the function is y = 2. Since the function is even if we plug in -1 for x the outcome is the same, y = 2. The graph tgrows faster than w.

 

 

After exploration of the positive coefficients of a parabola, the positive quadratic , the positivity of the parabola reminds me of an U. This U reminds me of a smile. Lets look at the negative coefficients of the equation.

The negative quadratic t is shown below where a = -1.

n

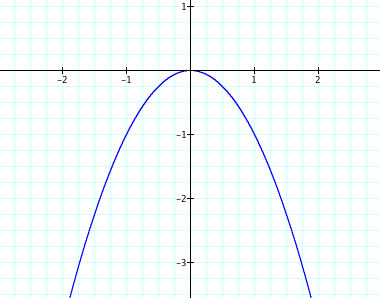
This is the graph wupside down, reflected across the x axis. Let's figure out why. Using the fucntion n, we plug in 1 for x, we get y = -1. If we look at the graph we can see that graph intersects at (1,-1). Moreover, this function is odd. Plugging in -1 for x, gives us y = -1. The graph intersects (-1,-1) too.

Change the values of a gives us a better idea for how the value of a affects the graph. Below are the graphs of    nega (in black) and ntx (in red). As we can see the graph of nega is wider than the graph n. The graph of ntx is slimmer than the graph of n. If we plug in 1 for x in both equations as before, we can see why the graphs behave as they do.

ne

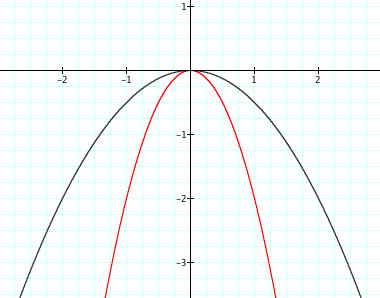
The negativity of the parabola reminds of an upside U. This upside down U reminds of a frown.

 

 

Lets explore the different variations of the coefficient a in the parabolic equation .

l

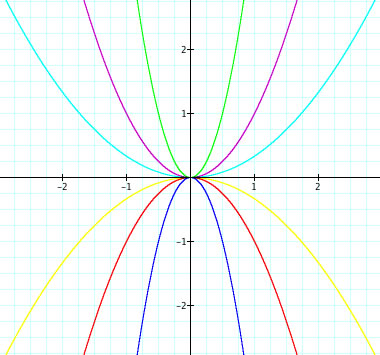
The graph of w is in purple. The negative of this equation is n. This graph is shown in red. This graph is reflected across the x axis. If we plot the points like we did before we can see why these graphs reflect each other across the x axis. The same goes for each graph here.

 

 

Changing the value a indicates how fat/thick/wide or skinny/thin/slim the parabola will be.

1)If the absolute value of a () is less than 1 then the parabola gets wider because the equation grows slower.

2) If the absolute value of a () is greater than 1 then the parabola gets slimmer because the equation grows faster.

So in all actuality the coefficient determines how fast the parabola grows.