Problem: A 4x4 picture hangs on a wall such that its bottom edge is 2 feet above your eye level. How far back from the picture should you stand, directly in front of the picture, in order to view the picture under the maximum angle? Side view:
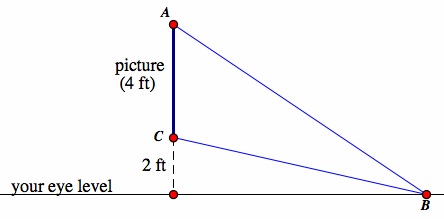
Solution: This problem is about optimal angles. We need to figure out where to move point B on the eye level line to make 
ABC as large as possible. We can see that if we move B very close to the picture, ABC gets very small, so we certainly should not stand there. If we move point B very far from the wall, ABC also gets very small. We can further explore the relationship of ABC to the position of B by looking at the circumcircle of 
ABC:
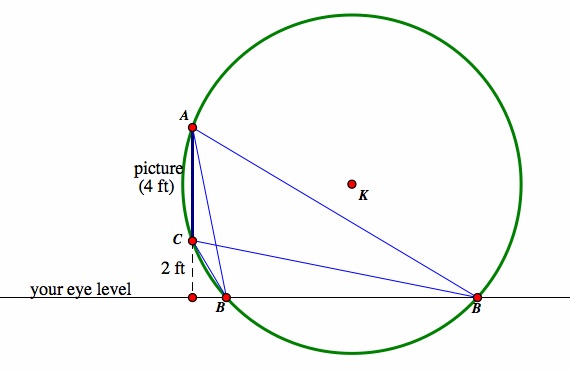
The measurement of ABC is exactly half of the measurement of AKC where K is the circumcenter of ABC. This fact is due to the Central Angle Theorem. Therefore, in order to maximize the measure of ABC, we need to maximize the measure of AKC. In order to do this, we need to minimize the size of the circumcircle of ABC. Since B is confined to the eye level line, we need to find the position of B where the circumcircle of ABC is tangent to the eye level line, like so:
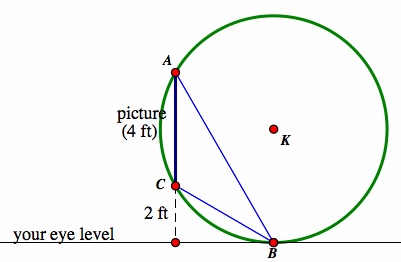
Since the circumcircle of ABC is tangent to the eye level line at B in this case, B and K are the same distance from the wall in this case. By definition, K must lie along the perpendicular bisector of AC, which means that it is exactly 4 feet off of the ground. Therefore, |BK| = 4 ft. As the circumcenter, K must be equidistant from A, B, and C, so we know that |AK| = |CK| = |BK| = 4 ft. We can see now that we have two sets of equilateral triangles in this problem, like so:
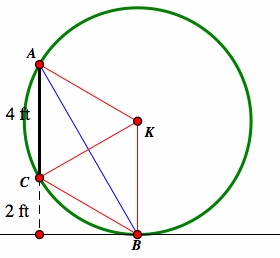
We know that AKC is equilateral because we have calculated all of its side lengths to be 4 ft. Since, C is 2 ft above eye level, |CK| = 4ft, and |BK| = 4 ft, and BK is perpendicular to the eye level line, we have sufficient proof to say that KBC is equilateral, which means that |BC| = 4 ft. We can use this fact, along with the Pythagorean Theorem, to conclude that the distance from B to the wall is 
= 
3.46 ft.
One other detail that we can notice about this problem is the measure of ABC. We know that AKC is 60 degrees because AKC is equilateral. The Central Angle Theorem tells us that ABC is half of AKC, making the measure of ABC 30 degrees in this optimum situation.