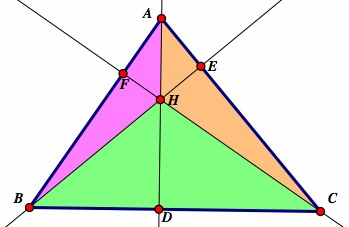
We will begin this exploration by looking at an acute triangle, 
ABC with orthocenter H, and points D, E and F being the feet of the perpendiculars from A, B, and C respectfully as such:
Proposition 1: 
Proof: Let k = the total area of ABC. So:
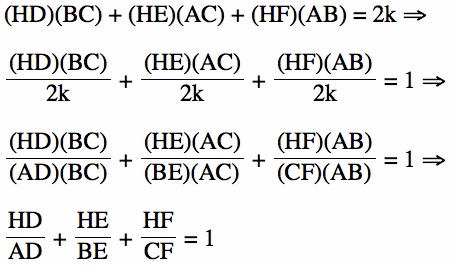
Proposition 2: 
Proof: Using Proposition 1, we can see that:
Note that these two propositions are true for all acute triangles because they only use the fact that the orthocenter H is inside ABC.
If ABC is a right triangle, then H lies on the vertex that contains the right angle, which means that neither of these propositions makes any sense.
If ABC is an obtuse triangle, the H will be outside the triangle ABC. Since the proofs for these propositions are area based, the proofs fail when ABC is obtuse. Furthermore, Proposition 1 is false for every acute triangle. This is because if A is the vertex that contains the obtuse angle, then HD
AD, which means 
1. Therefore, since lengths are never negative, 
1 for any obtuse triangle.