Spiral of Theodorus
Elizabeth Nelli
The spiral of Theodorus (also referred to as the square root spiral or the Pythagorean spiral) is a construction of continuous right triangles into a spiral. Each triangle has a side length of one representing the 
of the Pythagorean theorem, with the other sides filling in the spaces for the 
and
in the theorem.
To create the spiral on GSP:
First, using the grid view, create a triangle at points (0,0), (1,1), and (1,0). Next clicking on point (1,1) and the hypotenuse, create a perpendicular line. Then clock on points (1,1) and (1,0), respectively, and construct a circle by center+point. The next triangle is created using points (1,1), (0,0) and the intersection of the perpendicular line with the circle. Continue this process until the spiral is completed. Remember, each outer facing edge of the triangles making up the spiral must have a length of 1.
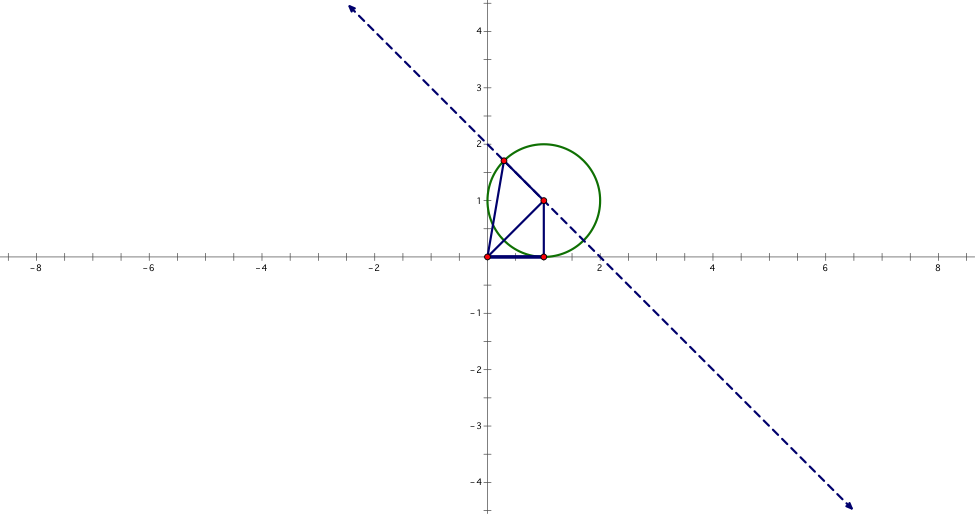
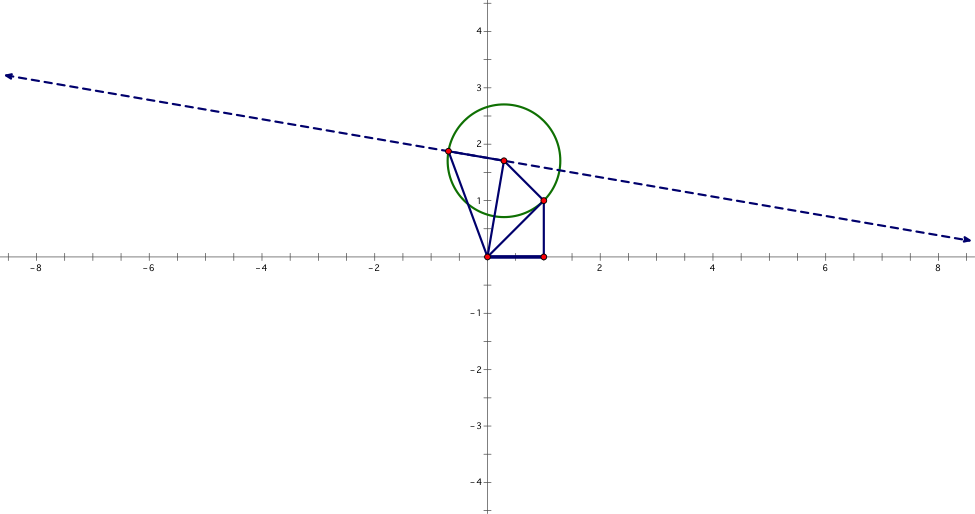
A finished spiral will look like this.
Theodorus used this spiral to prove that all non-square integers from 3-17 are irrational. The original spiral stops at √17 because that is the last hypotenuse before overlapping the rest of the figure. However, much later Erich Teuffel proved that no two hypotenuse’s will ever overlap regardless of how far the spiral continues. The side lengths of 1 will also be extended into a line that will never pass through any other vertices of the figure.
Growth rate of the spiral:
There are two different growth rates represented in the spiral: the angle and the radius.
Angle:
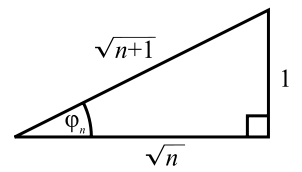
If αn is the angle of the nth triangle, then tan (αn)=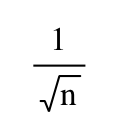 
and the growth rate of the angle αn of the consecutive triangle is αn=arctan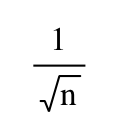
Radius:
Growth of radius at a certain triangle n is 
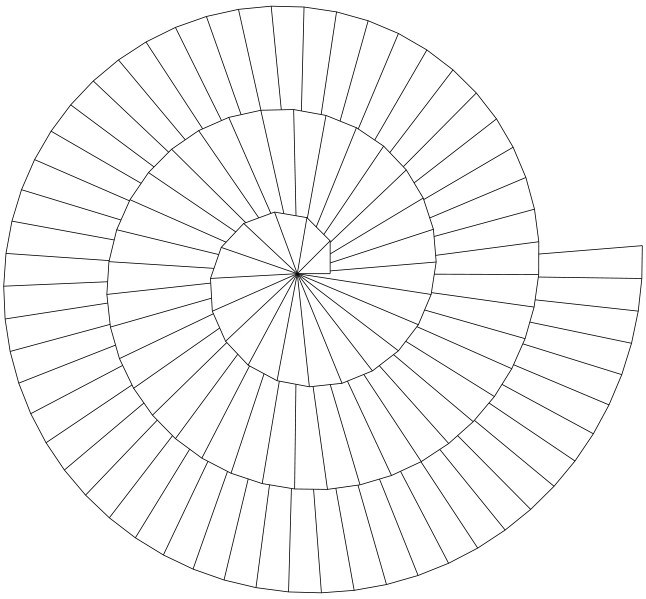
Division of a circle into 5 equal parts:
The spiral can also be used when solving the problem of how to split a circle into 5 equal parts. We begin by creating the radius of the first circle, which is √1. From there, just by creating the rest of the spiral we can create the other radii of the larger circles.
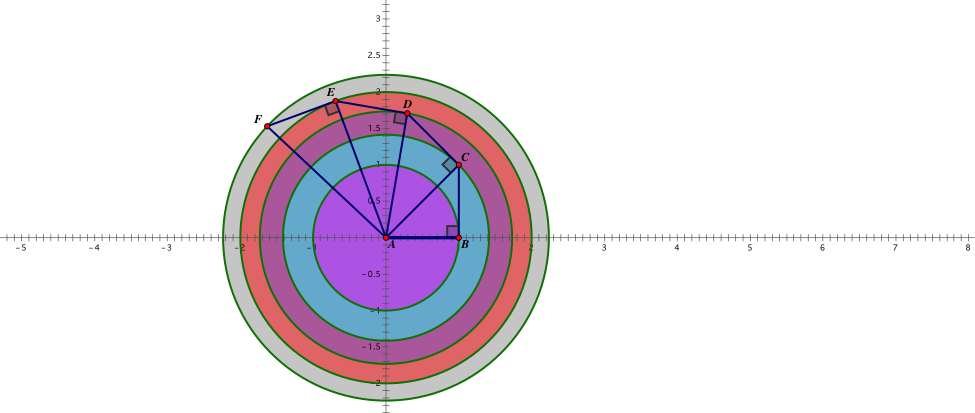
We can see using GSP calculations that all the areas of the 5 circles are equal. We start with the area of the inner most circle AB. Next, we calculate the area of circle AC. From there, were subtract the area of AB from the area of AC to see that the two are equal. This process can be done for each consecutive circle, by subtracting the area of the circle lying directly on top of it.
