Kristin Ottofy
Assignment 11
1. Investigate
Note:
-
When a and b are equal, and k is an integer, this is one textbook version of the " n-leaf rose."
Compare
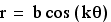
for various k. What if . . . cos( ) is replaced with sin( )?
This is the graph for variations of the function r = a + bcos(kθ) when a = b = k = 1.

When a=b=1 and k=4:

From the looks of it, for each unit increase in k, the number of "petals" on the rose increases by 1. For example, when k = 4, the "rose" shows 4 petals for each equation.
What happens when we change the values for a and b but keep them equivalent?
Here is a look at when a=b=2 and k=1.

The length of each petal has increased.
Next are graphs of when a=b=1 and k is a rational number.
When k = 0.2:

When k is not an integer, it appears that the equations no longer make petals but "spirals".
When k = .5:

At this point, some of the spirals have split and taken on a different shape.
When k = .9:

The closer k is to an integer, the bigger the spiral becomes until it forms a petal as shown in the image when a=b=k=1. Four petals formed in that image, one for each function.
Here is a video of changing k from 0 to 2 as a=b=1.
Notice how there is a point in time in which k is a value that causes different function to "align".
This can be seen in the following image when a=b=1 and k=1.75:

It turns out, that this occurs when k is a multiple of .25 and a=b=1.
In the previous image, 7 petals have formed.
Looking at it mathematically, with integers before, each function created k petals. Now, we have k=1.75, so each partial petal is 7/4ths of a whole petal.
Conclusion: The number of petals formed by each function depends on k when a=b and partial petals can be aligned when k is a multiple of .25.