Assignment 11
Polar Equations
Amena Warrayat
Problem 1 states:
Investigate
Note:
- When a and b are equal, and k is an integer, this is one textbook version of the " n-leaf rose."
- Compare with
for various k. What if . . . cos( ) is replaced with sin( )?
_____
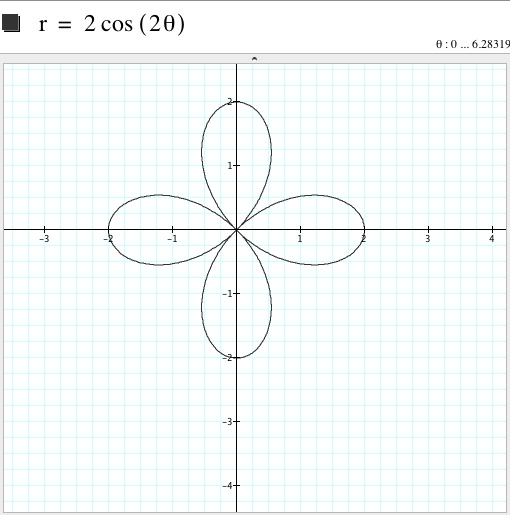
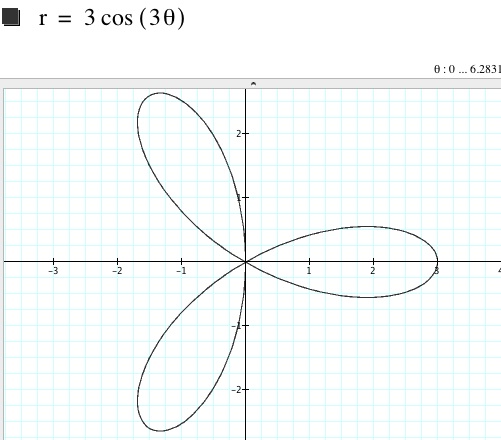
Let’s start with a =1, b =1, and k = 1
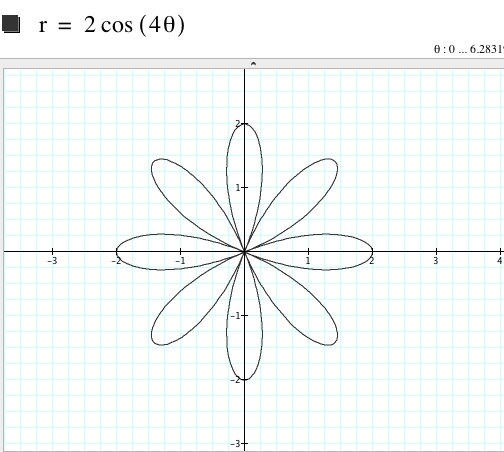
Let’s try changing the value of k, but keeping a and b constant.
From the graphs above we can deduce that k corresponds to n, where n represents the number of leaves on the n-leaf rose. Also notice that the x-intercepts of each graph is 2, and in some cases -2, which is the value of +/- (a+b).
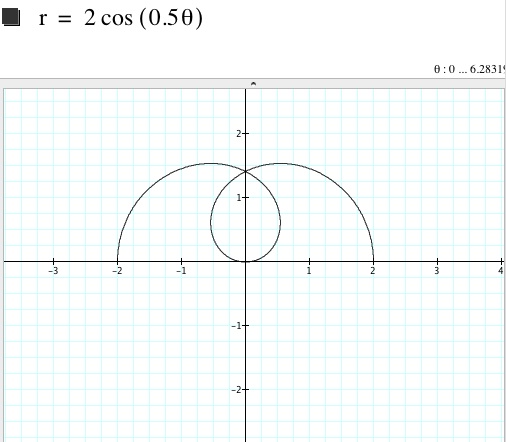
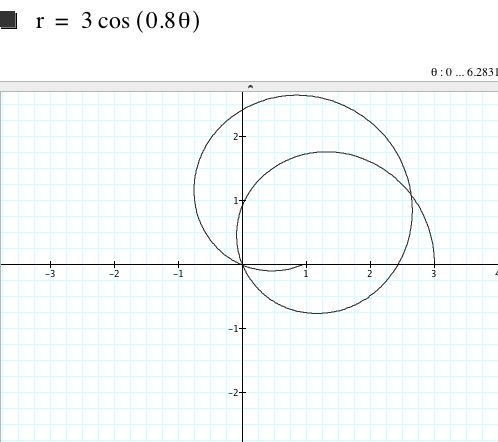
If we let k= .5
You must double your rotations to get a complete graph. We can see there are 2 inverted leaves.
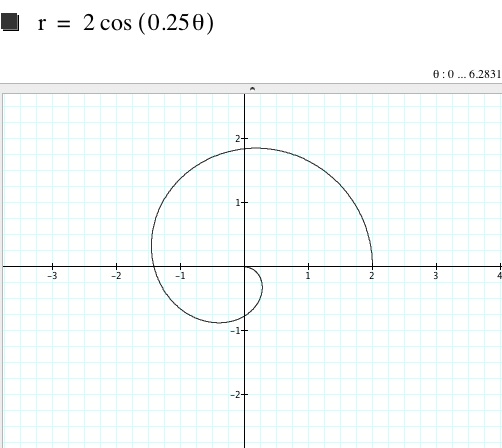
When k = .25
We must increase the # of rotations by 4 to get a complete graph. Notice that we now have 4 leaves inverted in each other.
Now let’s look at graphs of when the values of k and b are varied and a is the constant.
Now we have a double leaf rose. Notice k = n for small leaves as well as k = n for larger leaves.
Notice that the x intercepts are still equated to +/- (a+b), and as b increases the length of the second set of leaves elongates.
What if cos() is replaced with sin()?
The shape of the graph stays the same but when the translated from cosine to sine the graph is rotated 90°. It can also be noted that when a = b, the range of r is from 0 to 2a. On the other hand, when a ≠ b, r takes on negative values and hence the second set of leaves is produced.Now, let a = 0 and we can compare our previous results using the equation
with a ≠ b and k a real number.
It is interesting to see that by using the equation
, having a ≠ b does not guarantee the second set of leaves being produced!
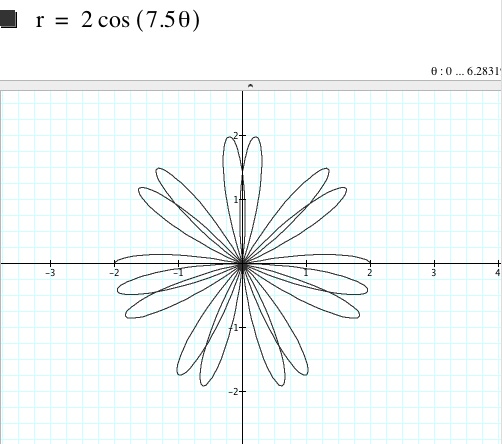
Now, let's explore
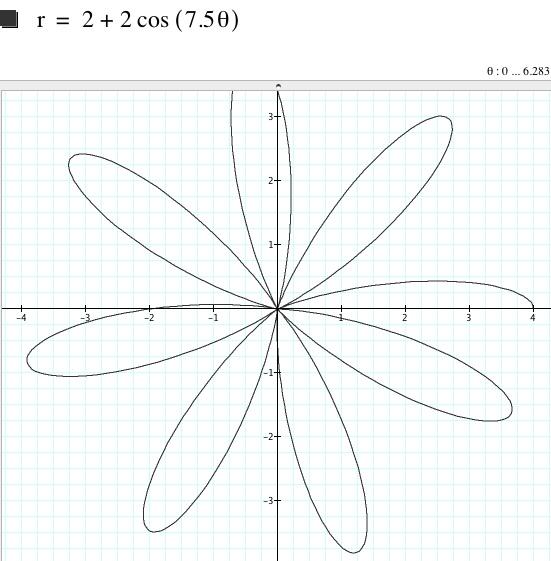
with k = 7.5. Is it a 7.5 leaf rose?
It is to be noted that when k is not an integer, it does not always form a k-leaf rose. Here, upon choosing the specific value of k = 7.5, we have three cases:
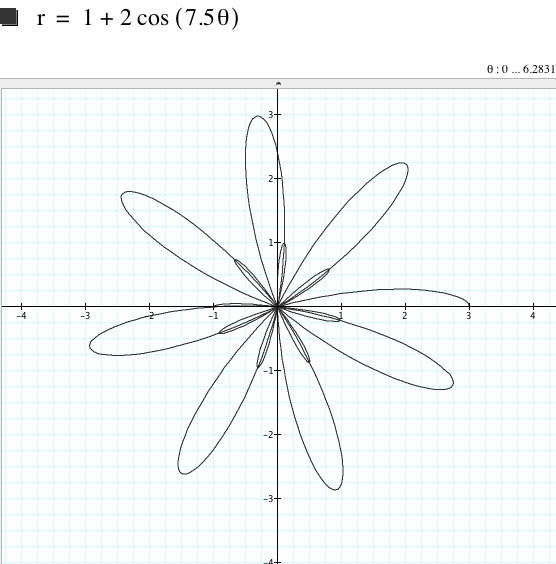
Case 1: a ≠ b, a = 0: two 7.5 leaf roses are disfiguredly formed.
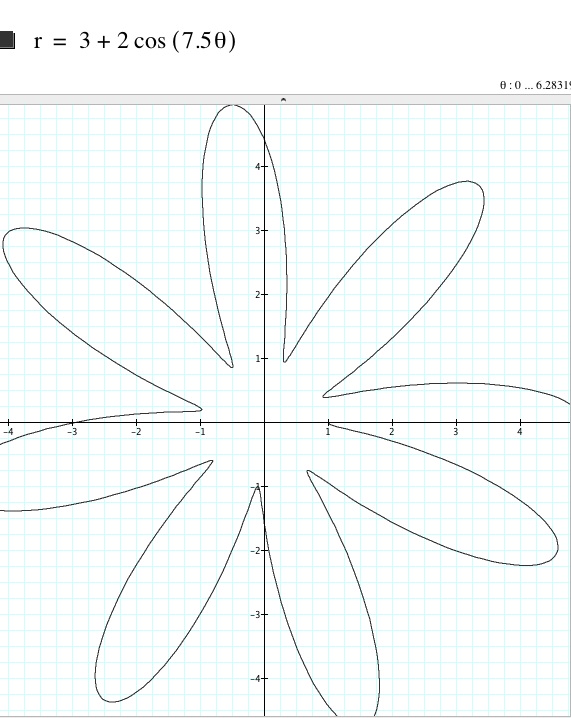
Case 2: a ≠ b, a ≠ 0, and a < b: a second set of leaves are formed.
Case 3: a ≠ b, a ≠ 0, and a >b: a 7.5 leaf rose is not fully formed because the vertex of the rose is not at the origin.
An exciting topic!