

Investigation: Show the relationship between the two standard forms of the graph of a parabola:
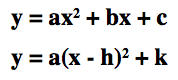
Part 1: Let's start the write-up with a derivation of
.
Now, using the following formula for the vertex, we can substitute (h, k) into our above equation.
Essentially, we see that given
our equation becomes:
Part 2: An interpretation/rationale for the value of parameters a, b, c, h, and k.
In the equations
,
h and k are the x-coordinate of the vertex of the parabola and y-coordinate of the vertex of the parabola, respectively. Their equations are written above.
Parameters a, b, and c:
The coefficient a controls the speed of increase (or decrease) of the quadratic function from the vertex. If a > 0, then the larger the value of a, the faster the function increases and the more the graph appears closed. Whereas, the coefficient b when combined with a affects the axis of symmetry and vertex of the parabola. The coefficient c controls the height of the parabola. More specifically, it is the point where the parabola intersects the y-axis.
The coefficients b and a together control the axis of symmetry of the parabola (which is also the x-coordinate of the vertex). The formula is
.
We note that the vertex is also the maximum point if a < 0 or the minimum point if a > 0.