1. The centroid (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
Using Geometer's Sketchpad (GSP), I have constructed the centroid (G) below for various shapes of triangles.
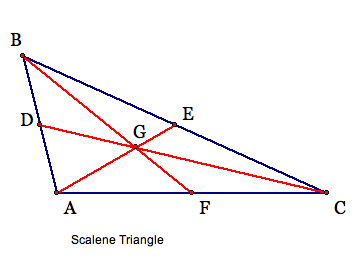
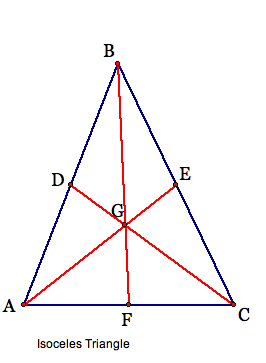
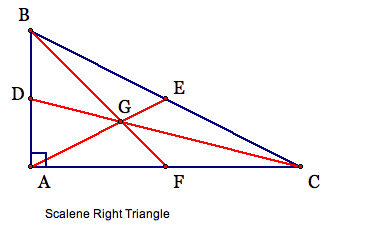
Specifically for right triangles, we see the centroid (G) in these circumstances as follows:
Now, I will prove Ceva's Thereorm and afterwards show that the concurrency of the medians is a corollary of Ceva's Theorem.
Statement of Ceva's Theorem: If three Cevians AE, BF, and CD are concurrent at G, then
.
Proof of Ceva's Theorem:
Notation: A(AGF) = Area of triangle AGF.
Now, we assume that the Cevians AE, BF, and CD are concurrent at G. We will show that
Looking at triangles AGF and CGF, we see that segment GF is the height for both of these triangles. Call this height h.
Then,
and
.
(equation 1)
Similarly, looking at triangles BAF and BCF, we see that:
(equation 2)
From equation 1 and equation 2, we see that:
(equation 4).
Now focusing on the other two sides of the triangle, we will write down the next two equations as the ratios of the appropriate areas.
(equations 5 and 6)
Taking the product of 4, 5, and 6, we have that
. Q.E.D.
We note that the converse of Ceva's Theorem is also true. In other words, if
Since Ceva's Theorem has been proved, to show that concurrency of the medians is a corollary of Ceva's Theorem, we simply use the aforementioned converse.
Statement: Medians of a triangle intersect at a point of concurrency.
Details:Let AE, BF, and CD be medians of the triangle ABC. Since the medians connect vertices to the midpoints of the edges of a triangle at opposite sides, we see that
.
So each of the ratios are 1 and therefore so is their product. Using the converse of Ceva's Theorem, we have that the medians AE, BF, and CD are concurrent. Q.E.D.
Return to Amena's homepage
