

We first perform the following constructions:
Note: The constructed orthocenter at each step is the orange point, denoted H.
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC. 4. Construct the Orthocenter of triangle HAB. 5. Construct the Orthocenter of triangle HAC. 6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC
Now, on to Investigation #6:
Given acute triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully.
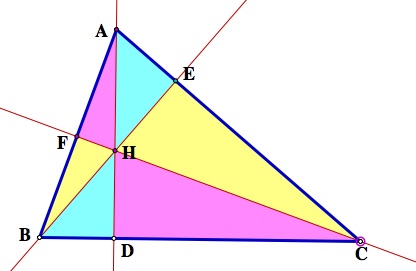
Proof of (i):
Given triangle ABC, as shown by the construction above, the orthocenter of this triangle is denoted as point H. So, let points D, E, and F be the feet of the perpendiculars from A, B, and C, respectfully. To start, consider the formula for the area of a triangle. Specific to this case, we have:
Which implies that:
(*)
However, keep in mind we also know that:
Now, examining our smaller triangles, we see that:
Which gives us another way to calculate area:
Using (*), let's divide (*) by AD*BC to get
which upon cancellation of BC, is the same as:
(**).
But since it is true that
, (**) can be rearranged into
.
Upon cancellation of AB and AC, we end up with:
.
Proof of (ii):
Using the proof of (i), we assume that
is true.
Then, from the triangle ABC and using the Segment Addition Postulate, we see that:
. Equivalently, this is
(***)
So, substituting the formulas in (***) into (i) provides the following situation:
.
What if ABC is an obtuse triangle?
First, I start with an obtuse triangle ABC and then construct points D, E, F, and H.
Observe that the length of HD is larger than the length of AD. Therefore,
But this is a contradiction (it is not possible for that sum to be less than zero).
Thus,
does not hold for obtuse triangles.
A similar argument can be constructed showing that the equation
also does not hold for obtuse triangles.