

Polar Equations
Colleen Foy
For exploration 11 I chose to investigate the following polar equation.
Note:
for various k. What if . . . cos( ) is replaced with sin( )?
Let's investigate these polar equations using graphing calculator. Note that for these graphs, a = b = 1.
k = 1.
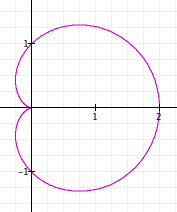
k = 2, k = 3, k = 4
By looking at the graph we can see that all of the graphs touch the x-axis at (2,0). Also, the value of k appears to determine the number of petals in the graph.
Let's see what happens when we keep k and a constant and vary b.
Note that as the b gets larger (in absolute value), the graph stretches. When b is negative, the graph flips across the y-axis.
Let's see what happens when we vary a but keep b and k constant.
It may be hard to tell, but the purple and gray graph are the same, the red and yellow graph are the same, and the and light blue graphs are the same.
In the graphs above, k = 1. What happens when we change the value of k.
It appears that as a gets larger than b, the graph becomes more of an ellipse. When b is larger than a, the graph has four petals and expands or stretches accordingly.
Similarly, when k = 4, we have a double 4 petaled flower, only when b is greater than a. When a is greater than b the graph doesn't cross itself and it seems to be approaching the shape of a circle.
Let's examine the idea that as a becomes larger than b, the graph expands towards the shape of a circle.
I am not sure if it will ever become a circle exactly, but that would be worth investigating.
Now, what does the graph look like when we eliminate the parameter a?
Now if we vary k and keep b constant:
Note that k still determines the number of petals. However, when k is odd the number of petals is k, but k is even the number of petals is 2k.
What happens when we change the original equation to
?
It appears the be the same shape, but now it is centered on the y-axis instead of the x-axis.