

Centers of Triangles: GSP Tools
by
Sarah Major
Orthocenter
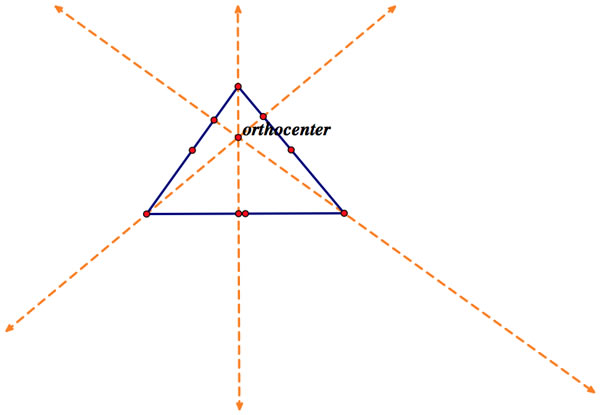
This can be constructed by finding the intersection of the altitudes of the triangle.
Circumcenter
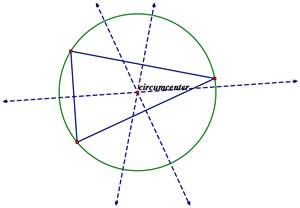
First, find the midpoints of each side. Next, construct perpendicular lines through the midpoints. These are the perpendicular bisectors. The intersections that result are the center of the circumcircle. Go on to construct the circumcircle by drawing a circle that passes through the midpoints of the sides of the triangle. One will find that only two perpendicular bisectors are needed to find the circumcenter for a given triangle.
Incenter
This is constructed by finding the intersection point for the angle bisectors of the three vertices of a triangle. The resulting circle, or incircle, is tangent to all three sides of the triangle.
Centroid
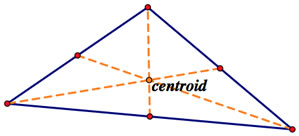
This can be found by first finding the midpoints of each side of a triangle and then creating segments with each midpoint’s opposite vertex. The resulting intersection is the centroid. This is ideally the “balancing point” for the triangle.
Exeter Point
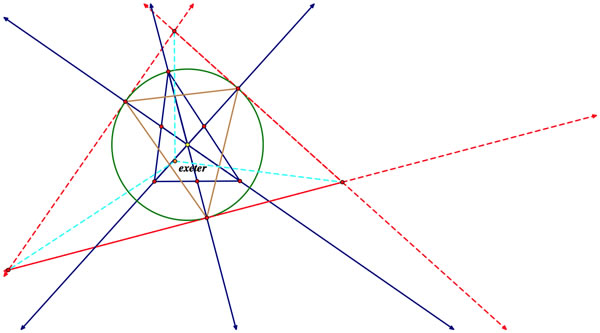
This construction can be confusing, but if one takes it step by step, it is fairly simple. Start with any triangle and construct the lines necessary to find the centroid. Construct a circle whose center is the centroid and has a radius that is the length from the centroid to the vertex that is farthest from the centroid. Where the lines from the centroid construction intersect the circle will be the vertices of a new triangle. The centroid of the original triangle is now the circumcenter of the new triangle. Now, construct a triangle whose incircle is the circumcircle of the second triangle. Construct the centroid for this new triangle. This is the exeter point.
Center of the Nine Point Circle
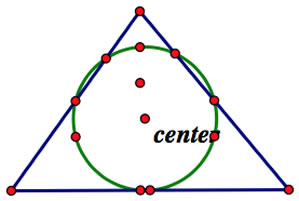
The center can be found by constructing the nine point circle. The significant nine points are: the three midpoints of the sides of the triangle, the three feet of the altitudes of the triangle, and the three midpoints of the segments produced by the intersection of the altitudes with the sides of the triangle and the orthocenter.
Euler Line
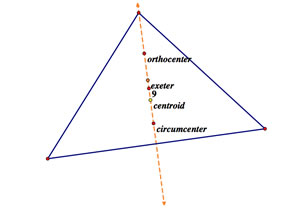
This is self-explanatory. This is the line which passes through the orthocenter, exeter point, centroid, circumcenter, and the center of the 9 point circle for a given triangle.