

Trying Trisections
Seven Ways to Trisect a Line Segment
by
Sarah Major
The prompt for this exploration was to find seven ways to trisect a line segment and to provide evidence that the segment has been trisected. Though some of my methods are similar, I have discovered these seven ways and have outlined them below.
Method 1
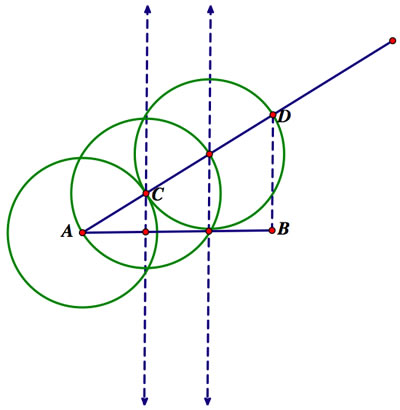
This is one of the simpler methods we have discussed in class. Given segment AB, construct a segment extending from the endpoint A (make sure this segment is particularly long). Construct a circle with center A passing through the segment at some point before point B. Construct a second circle whose center is the point at which the first circle intersects the same segment (say, point C). Repeat this process to construct a third circle.
Draw a line segment from the point at which the third circle intersects the second line segment (say, point D) to B. Construct parallel segments from point C and the other point where the circles intersect to the original line segment. This trisects AB.
More information on this construction can be found by following this link: Other Constructions
Method 2
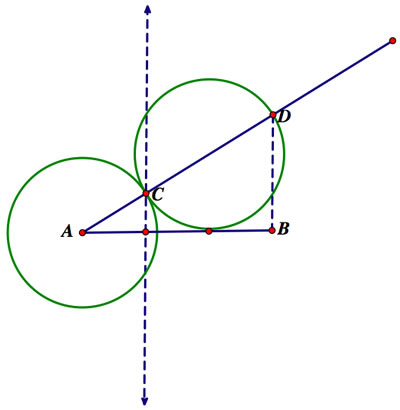
A similar method uses the same construction, but there is no need for the second circle. Instead, construct the first circle as instructed. Draw a second circle that is the same size but who intersects the second line segment at point C. Draw the first segment from the second circle to point B and a parallel segment from point C to AB. Find the midpoint of these two intersection points, and segment AB is trisected.
Method 3
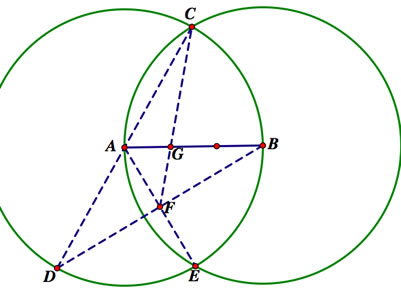
Construct two circles whose radii are the length of the segment but the right end of the first is the right endpoint, and the left end of the second is the left endpoint. In essence, you’re attempting to bisect the line segment. Find one of the points where the two circles intersect (say, point C) and construct the diameter from point C. The other endpoint of the diameter is point D. Construct the radius from point A to the other point where the two circles intersect (point E). Now, construct the chord extending from point D to point B. The point where DB intersects AE will be point F. Now, draw a segment from point F to point C, and label it’s intersection with AB as G. Find the midpoint from the segment resulting from extending G to B. The segment AB has been successfully trisected.
Why does this work? We know that ADE and ABE are both equilateral triangles because all of the sides result from radii of the two congruent circles. Therefore, angle DAF is congruent to angle BAF. By SAS theorem, we can say that triangles DAF and BAF are congruent. In saying so, segments DF and BF must be congruent, and we know that segments CA and AD must be congruent (because they are the two halves of a diameter). So, segments AB and CF are medians of triangle BCD. This makes G the centroid because it is the point at which these medians intersect, and the centroid is 1/3 the distance along the median AB.
Method 4
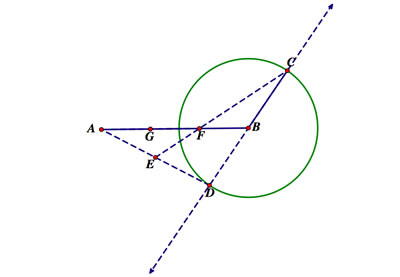
Construct a segment extending from point B and label its other endpoint C. Construct a circle with a radius of BC. Where the diameter extending from BC intersects the other side of the circle, label this point D. Construct the segment from D to A and find its midpoint, E. Construct the segment from point C to point E. Where this segment intersects AB, point F, trisects the segment. Find the midpoint between A and F to find the other trisection point.
Why does this work? We can construct the triangle ACD by constructing the segment from A to C. We know that E and B are the midpoints of two sides of this triangle, and so we have essentially constructed two medians. F is the point where these two medians intersect, so this is the centroid of this triangle. The centroid is 1/3 the distance along the median, AB.
Method 5
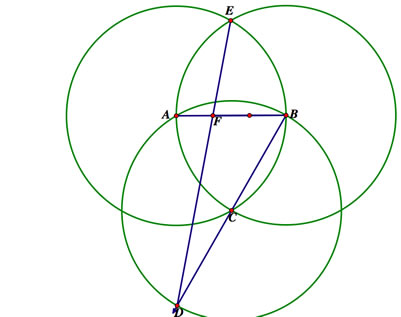
Construct two circles with radius AB, one passing through A and one passing through B. Next, construct a circle with the same radius passing through A and B. Label its center C and draw the radius BC. Construct the whole diameter and label the other endpoint of the diameter D. Label the other intersection of the first two circles as E and draw a segment from D to E. Where this segment intersects AB trisects the segment and is labeled F. Find the midpoint between F and B to find the other trisection point.
Why does this work? If we were to draw the segment AE, we would see that triangle AFE is similar to triangle BFD. With the smaller triangle, side AE is the radius, and BD is the diameter, so BD = 2AE. Therefore, BF = 2AF, which means AB is split into three equal parts.
Method 6
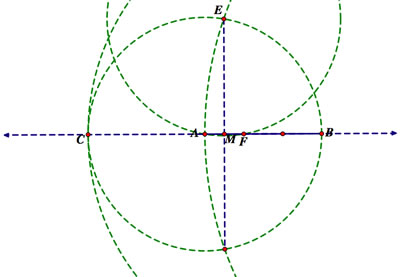
First, extend AB to the line it lays on. Construct a circle with a radius that is AB. Label the point at which it intersects the line as C. Next, construct a circle with a radius is CB. Label its intersection with the line as D. Next, construct a circle whose radius is AD. Label its intersection with the first circle as E and its intersection with the line AB as G. Last, construct a circle whose radius is AE. The point at which it intersects the segment AB is its trisection, and it can be labeled F. Find the other trisection point by finding the midpoint between F and B.
Why does this work? We first look at angle AEG. We know this is a right angle because of the inscribed angle theorem. This angle subtends a diameter, so it must be 90 degrees. Also, notice that we can construct a chord from E to the other intersection point below AB. We can label where it intersects AB as M. This is actually a perpendicular bisector of AF, so angle AME is also a right angle. Therefore, triangles AME and AEG are similar triangles. Also notice that because M is the bisection point of AF that AG = 6AE. Since we have similar triangles we can have the following ratios:
AG/AE = AE/AM
It follows that AM = 1/AG = 1/6 from our earlier observation. We established that point M is the perpendicular bisector point, so AF = 2AM = 1/3.
Method 7
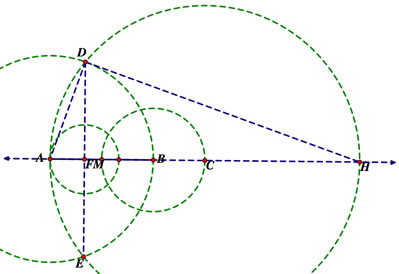
First, extend segment AB to be a line so that points past the segment can be utilized. Find the midpoint of segment AB. Construct a circle passing through this midpoint with a center at B. The point at which the circle intersects line AB is C. Now, draw a circle with radius AC passing through A and also a circle passing through B with center A. Where these two circles intersect, draw a segment between these two points and label them D and E. Where segment DE intersects AB, label this point F. Now, construct a circle passing through A whose center is F. Label the point where it intersects segment AB as G. Points F and G trisect the segment.
Why does this work? It took me a long time to figure out why. I only knew that it worked because I could construct a circle through G with the same radius as the circle with center F and it passed through B. After a while, however, I figured out why it works. For the sake of this tentative proof, let’s label the midpoint of the segment as M.
We know that AM is congruent to MB, which is also congruent to BC because it is the other radius that is in the same circle as the radius created by MB. Therefore, these three segments are congruent. We can therefore say that AC = 3AM.
If we construct the intersection of the circle with radius AC and label it H, we can say that 2AC = AH. Since AH = 3AM, we can say that AH = 6AM.
If we construct the radius AD, we first notice that is also a radius of the circle that AB is also a radius to, so AD = AB. Furthermore, we can see that the segment DH is actually tangent to the circle with this radius and passes through the same point, D, so this tangent segment is perpendicular to the radius AD. Therefore, the triangle ADH must be a right triangle. DF is also perpendicular to AH, and so we have created similar triangles AFD and ADH.
With this knowledge, the ratio of any side of one triangle to its corresponding side on the other triangle must be in the same ratio as all of the other corresponding sides. We can thus set the ratio of the two small legs to the ratio of the two hypotenuses:
AF/AD = AD/AH
We have an AD on both sides, and we know that AD = AB, so we can substitute.
AF/AB = AB/AH
We know that AH = 6AM, so we can substitute.
AF/AB = AB/6AM
We know that AB is split in half by the midpoint M, so AM = BM, and 2AM = AB, so we can substitute:
AF/AB = 2AM/6AM, or AF/AB = 1/3
So the length of AF is 1/3 the length of AB.