

Write-Up #10
Parametric Equations
By Jaepil Han
2. For various a and b, investigate
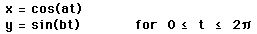
(1) Varying a from 1 to 5 for integer values
If a goes large, then the curve of the parametric equation has more frequency than before. However, the curves located only between y=-1 and y=1. As we may know, when the parameter a is 1, x2+y2=1 because (cost)2+(sint)2=1. Also, When the parameter a is 2, x=1-2y2. And so on. Interstingly, when the parameter a is even the graph has a continuous loop. When the parameter a is odd the graph hasn't a continuous loop.
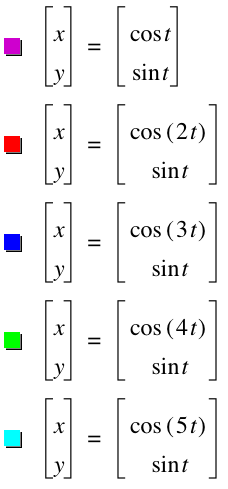
Here's the graph of the parametric equation when a=50.
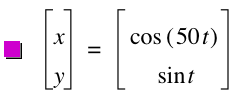
(2) Varying a from 1 to 5 for integer values
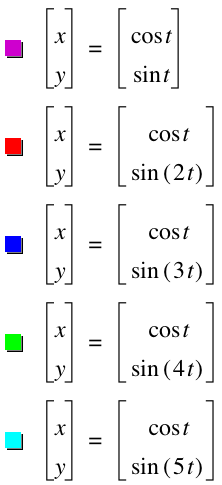
Similarly, the value of b getting greater, the curve of the parametric equation has more frequency.
Here's the graph of the parametric equation when b=50.
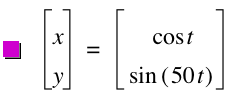
Even we change the values of a and b, it only changes the frequency of the curves. All the curves generated by the values of a and b make a sort of square.
Here's the graph.

Here's useful links releated to Lissajous-curves.
Lissajous-curves by WolframMathworld