Write-Up #11
Polar Equations
By Jaepil Han
1. Investigate r = a + bcos(kθ)
(1) When a and b are equal, and k is an integer, this is one textbook version of the " n-leaf rose.
* when a and b are equal, and k=1
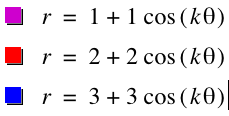
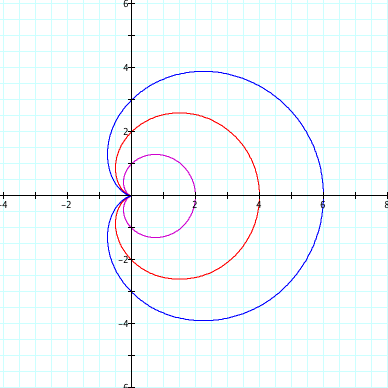
When the value of k is 1 and the value of a and b are equal,
the value of a and b is bigger, the graph of the equation is bigger. It is acting like a scale facter of the graph of it.
* when a and b are equal, and k = negative integer
When k is negative integer, the graph of the equation is the same as the graph of the one when k is positive integer. Here's an algebraic explanation.
Assume n = natural number which is -n = k
Then, r = 1 + 1cos(kθ) = 1 + 1cos(-nθ)
Since cosine is an even function, r = 1 + 1cos(nθ)
Therefore, the graph of r = 1 + 1cos(kθ) is the same as that of r = 1 + 1cos(-kθ)
Here's the graph of the equations when k = 1 and -1.
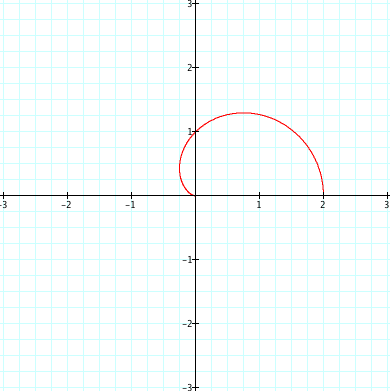θ: 0_π
As we may see, the graphs of the two equations are the same, and we may conclude that the graph of the equations when the k is positive integer and that of the equations when the k is negative integer are the same.
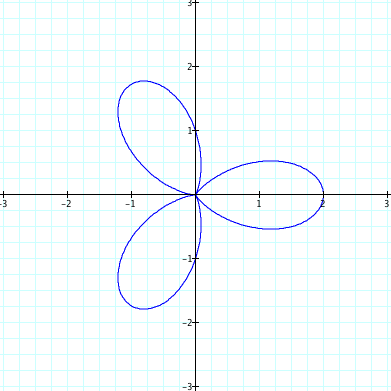
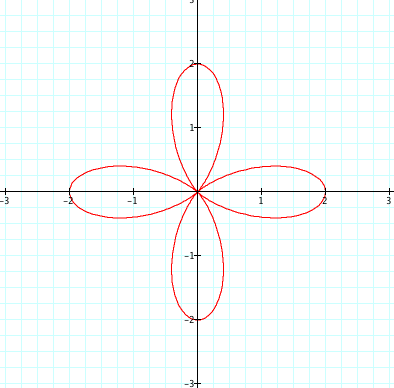
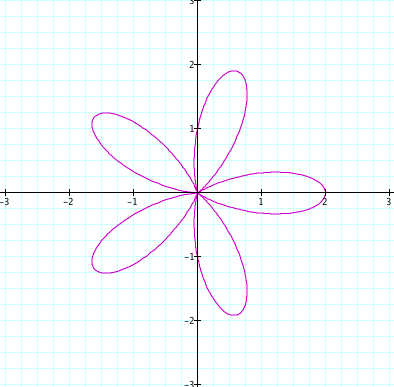
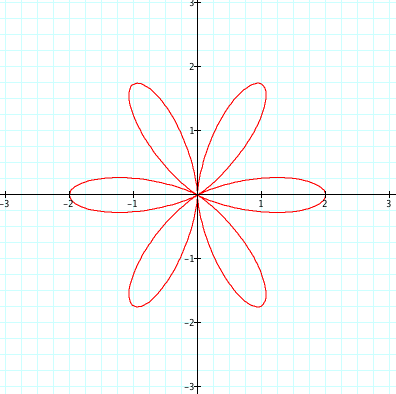
*when a and b are equal, and k = positive integer
When the value of integer k varies, the possible conjecture is that the integer value k represents the number of "leaves".
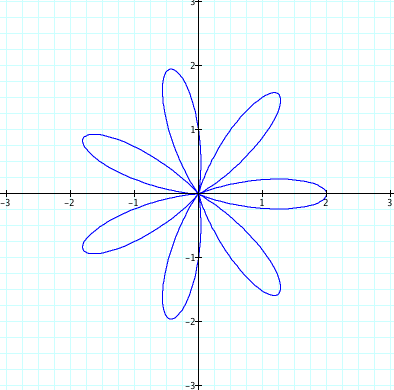
From those graphs, we can empirically hypothesize that the value of integer k represents the number of leaves.
(2) Compare with r = b cos(kθ) for various k.
Here are some graphs of the equation r = b cos(kθ).
* b = 1, 2, 3, 4, 5 and k = positive odd integers
when k=1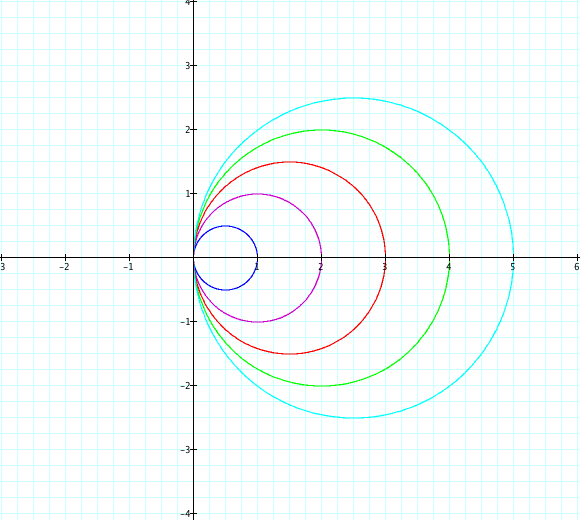 
when k=3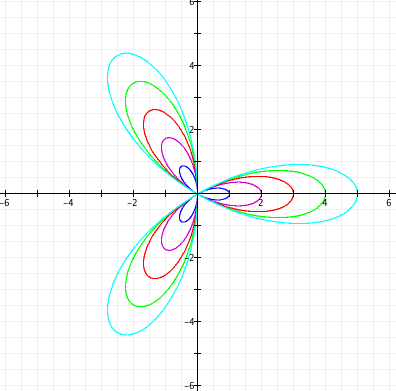 
when k=5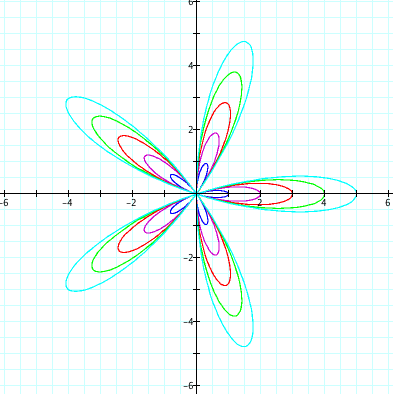 
It seems that the odd integer value of k in r=bcos(kθ) represents the number of leaves like the part (1).
* b = 1, 2, 3, 4, 5 and k = positive even integers
However, when the value of k is even, the graph of the equations are slightly different from the graphs above.
when k=2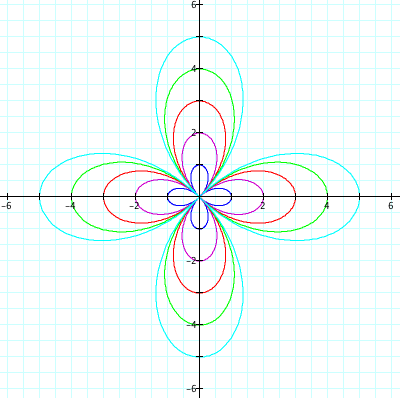 
when k=4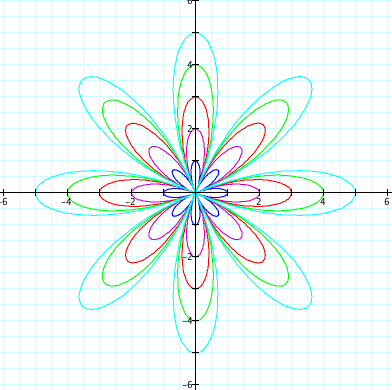 
when k=6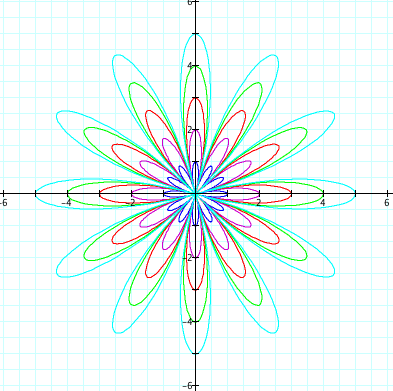 
Consequently, when k is even integer, the graph of the equations looks like the "2k-leaf rose," and the graph of the equations is symmetric respect to the x-axis, y-axis, y=x, and so on.
e.g. k=2 => 4-leaf rose
k=4 => 8-leaf rose
k=6 => 12-leaf rose