Objectives
Students will learn to graph and analyze using a line plot and work with mean, median, mode and range. Using Fathom the students will set out to predict and then determine of the four measurements collected will give the most accurate predictions and what can be concluded from the relationships built. The introduction of a best-fit line and what can this line tell will also be a key feature of the lesson.
Goals
1. Determine what relationships between measurements developed and what problems can be solved and conjectures can be made from these relationships.
2. Develop a clear understanding of what mean, median, mode and range tell us and cases when each should be used.
3. Introduce the use of scatter plots and mention other forms of plots such as box plots, line plots and histograms.
4. Analyzing plots so that best-fit line and linear least squares solution can be determined.
Materials
1. Fathom software
Procedure
1. Review what was accomplished yesterday in gathering data and determining that the data that was gathered from the class was valid. Also, ask the class two questions to ponder as you open Fathom to begin the exploratory exercise of the data collection.
Questions for students:
a) Name a few ways that we could ensure that we could improve our predictions?
b) If you do no have access to Fathom what are some other technologies that can be used to collect and analyze data?
Ask for responses to the questions posed and ask for explanations so that reasoning can be verified.
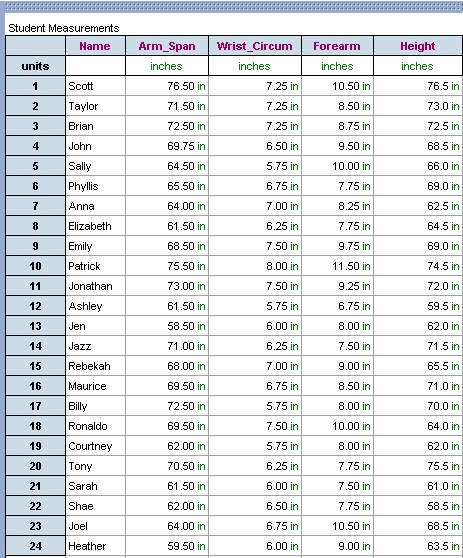
2. Open up the Student Measurement chart with all the information typed in. For instructions on typing in the information click here.
3. Give the students a few minutes to look at the data and collect thoughts on what is being observed.

4. After Fathom is opened show the students how to drag an attribute onto a new <graph> that was developed. The first graph that is created is a dot plot. Show the students how the different types of graphs can be created. Make sure that the students that these are single attribute graphs.
Dot Plot
Line Plot
Box Plot
Histogram
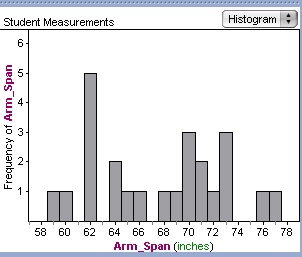
5. Have the students make some simple observations from the single attribute graphs. Begin a discussion of the differences between mean, median and mode. Also mention the term range and what it means. Make sure the discussion includes when the central tendency measures should be used to describe a data set. The following example would be useful to follow:
Example: Suppose we want to know the average income of a small number of parents. To simplify the calculations and to obtain the answer quickly, we randomly select 3 students as a sample at random. Let us consider two possible scenarios:
Case 1: Incomes - 25,000, 30,000, 35,000
Case 2: Incomes - 25,000, 30,000, 1,000,000
Compute mean and
median in each case and discuss which one is more appropriate.
The actual computations are pretty simple.
However for large sample sizes he mean and median tend to be close to one another so these are more likely to be used to describe the data set.
6. Following the discussion on measures of central tendency show the students how to create a two-attribute graph and then scatter plots can be developed picking any two categories. Dragging any two attributes onto the newly created graph will automatically create a scatter plot. One attribute can be dragged to the x-axis and the second attribute can be dragged to the y-axis. Ask the students to create these scatter plots and see what relationships develop between two of the attributes. The first question that needs to be asked is what one dot on the scatter graph represents (a student). Begin to call on students to see what is being observed and make sure that an in-depth discussion on relationships takes place. What relationships are developing between the four attributes?
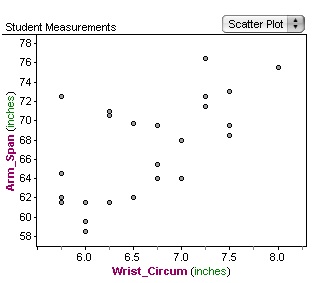
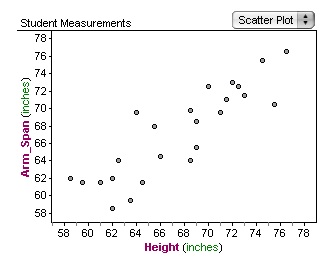
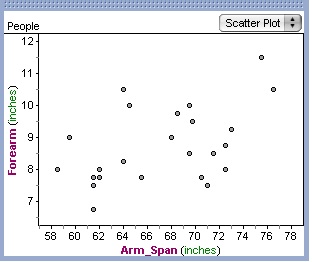
Here is a look at three sample scatter plots that the students may encounter. As you can see the plots are very different and different conclusions can be made with each.
6. During this investigation into the scatter plots continue the lesson by asking questions. The following questions can be addressed: 1. What does the data look like on the graph?; 2. What does the distribution of the data look like?; 3. What points look different from the other points on the plot (this is where athe outlier would be mentioned but probably not discussed)?; 5. What else is being observed?; 6. Could this data be set up differently?.
7. Continue the lesson be introducing the idea of a best-fit line. Explain what a best-fit line is and what it can tell you about the data. Ask a few students to come to the overhead (if possible) to draw a best-fit line on two or three of the graphs. While they are doing this ask the class if the students line is accurate and why the location of this line was chosen. Either validate that the student was correct or if the student was wrong start a discussion with the class about where an appropriate line would be placed.
8. Show the students how Fathom will draw a movable line for you and you can alter the line to where you might think the best-fit line may be most accurate. Here is a guess on where the best-fit line may fit on the Height and Arm Span comparison.
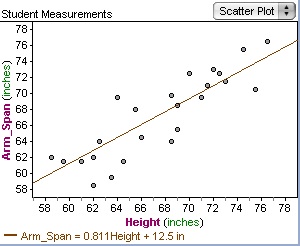
9. After making the guess on the best-fit line show the sum of the squares. Explain that by minimizing this sum will ensure that the best-fit line is most accurate. What is this sum? This is the sum of the linear least squares, which is mathematical technique used to optimize and approximate a solution to a system of linear equations that does not have an exact solution. Have a very detailed discussion on why this works and what it exactly means. Using the same graph as before have Fathom show what the least squares solution would be.
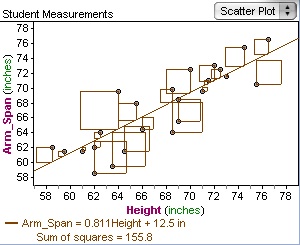
Then alter the movable line until the lowest sum of squares is found to see how close our best-fit line was to being accurate. As you can see the guess we made had a sum of squares of 155.8. Show the students how Fathom will show you the least square line and solution which is under the graph menu. The actual solution is 153.6 which is not that far off from our guess made earlier.

This will conclude the lesson but at the end of class review what was observed and concluded from mean, median, mode and range discussion and the introduction of the best-fit line and least squares solution. Make sure that the students have a clear understanding of this new terminology and what it means when describing data and linearity.
Rationale
During the class session students will be exposed to taking the data that was gathered and making sense of it. By exploring scatter plots students will learn the reasoning behind making conjectures and observations from a sample that they collected. From these scatter plots students can then start to understand the concept of a best-fit line and what that means to a linear equation. Hopefully through the questioning by the teacher the idea of linear equations and what slope means will be discussed. Although these two items are not the focal point of the lesson I would hope the students could connect the dots.
Also by divulging into this data analysis students can begin to think of when a relationship may develop between two variables and what predictions can be made if any. The homework that follows this lesson will explore the idea that sometimes attributes like this are related but other times linearity does not occur and predictions cannot be made.
Assessment
During class time student's responses to questions and participation will be noted and they will be graded objectively. The homework assignment following the activity will be the main tool used for assessment to see if the students understand the material or if more time needs to be spent on the lesson. The students can work on the homework during the last minutes so that any questions that arise can be addressed.
Homework
The students will be handed a copy of the homework worksheet along with a piece of graph paper. The homework instructions and worksheet are below.