Stephani Eckelkamp

The Parabola:  Friend of Foe?

 

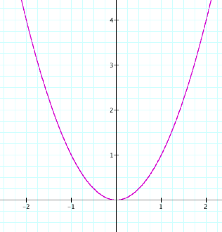
The graph of a parabola y=x2 has a vertex at (0,0).  The graph is shown below.

 

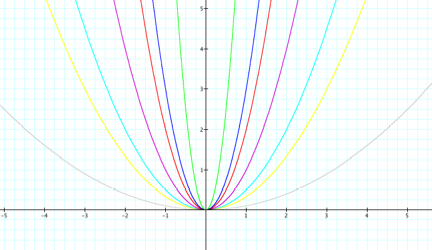
Now, let us look at the graph y=ax2, where a = 1, 2, 3, 10, ½, 1/3, and 1/10É

 

 

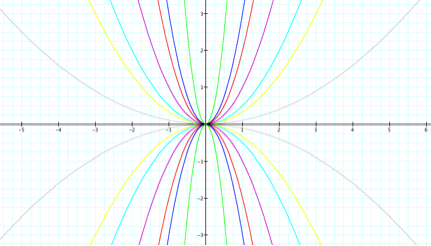
Éand when a = -1, -2, -3, -10, -1/2, -1/3, and -1/10.

 

 

y = 10x2 and y = -10x

 

y = 3x2 and y = -3x2

 

y = 2x2 and y = -2x2

 

y = x2 and y = -x2

 

y = ½ x2 and y = -1/2x2

 

y = 1/3x2 and y = -1/3x2

 

y = 1/10x2 and y = -1/10x2

 

 

 

 

 

 

We see that by increasing a the parabola is closing in on the y axis, and as we decrease a the parabola opens wider towards the x axis.  By changing a to a negative integer we get a reflection in the x axis.

 

LetÕs investigate sine functions as the variable a.

 

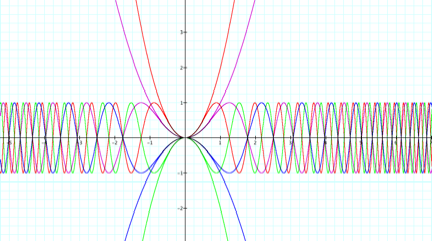Here we are looking at the following equations:

 

y = sin x2 and y = x2

 

y = sin 2x2 and y = 2x2

 

y = -sin x2 and y = -x2

 

y = -sin 2x2 and y = -2x2

 

The graph of the y = ax2 equation and the y = sin ax2 share the vertex of (0,0). 

 

 

 

 

 

 

 

 

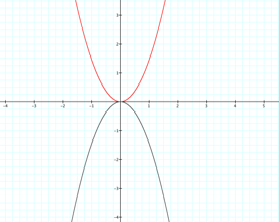An example of the graph to the right for all values of n from -10 to -.5 and . 5 to 10.  Animated graph                                                                                                                     

 

y = nx2

 


 
All graphs have a vertex of (0,0) because we are only working with the equation y = ax2.  From my investigations I can conclude that a (or n in the graph above) changes the width or narrowness of the parabola.  As we can see with the sin curves above, the wave lengths are closer together the greater a is.

 

 

Return