Sarah Hofmann

EMAT 6680 Summer 2006

Assignment 12

Project 4

Leonardo Pisano Fibonacci was a mathematician who lived in Italy from 1170 – 1250. He had many great accomplishments, but is most noted for his work with a particular recursive sequence now known as the Fibonacci sequence.

The Fibonacci sequence is defined as

f(0) = 1

f(1) = 1

↓

f(n+2) = f(n+1) + f(n)

We can use Excel to show the Fibonacci numbers.

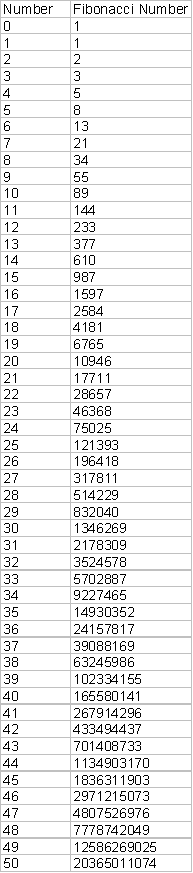
As you can see, the Fibonacci number increases quite quickly. But it might be interesting to look at the ratio of one Fibonacci number to the prior Fibonacci number.

We can see that this sequence comes to a limit very quickly. Why would this be true? Because f(n+1) = f(n) + f(n-1) and

f(n)/f(n+1)

f(n)/[f(n) + f(n-1)]

So each number is directly related to the previous number, so the ratio will level out. We can think of this as f(n) = f(n-1)+f(n-2) is to f(n-1) as f(n-1) is to f(n-2), which is the golden ratio phi = (1 + \sqrt(5))/2.

Now we’ll look at the ratio of every second term.

As we expected, the difference between every third value of the Fibonacci sequence is 1 plus the golden ratio, because we know that every element of the Fibonacci sequence is related to the previous elements.

All that the limit of these sequences seems to depend on is the fact that a value is directly related to the previous two values by f(n) = f(n-1) + f(n-2) as f(n-1) is related to f(n-2). If this is true, then the starting values of the Fibonacci sequence should not effect the limit of the ratios. Let’s try a few different starting pairs and see if this is true.

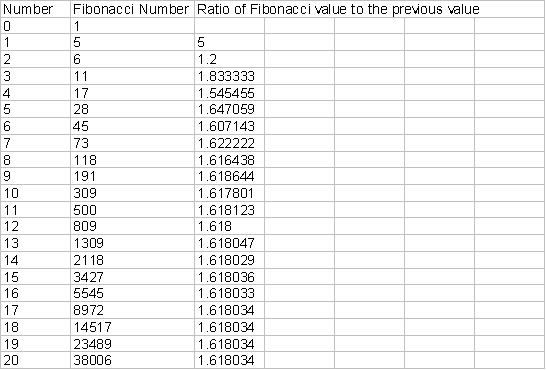
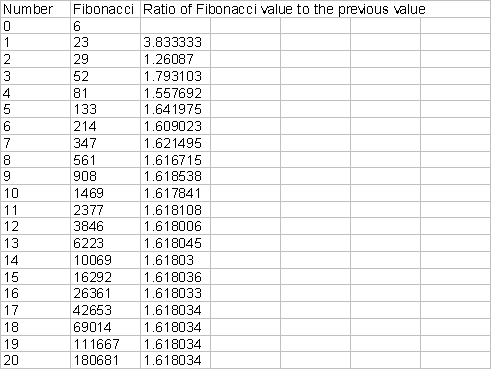
As we can see from the above three cases, the ratio is the golden ratio no matter what two initial values are chosen, as we anticipated.