
Visiting Polar
Equations
By: Damarrio Holloway
Summer 2006
Assignment 11
Problem #3
We have just recently visited with parametric equations and now we will go next door and introduce the Polar Equation family. Here, we will specifically investigate with different values of p for the following polar equation family:
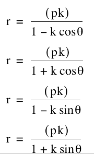
The characteristics of this family are as follows:
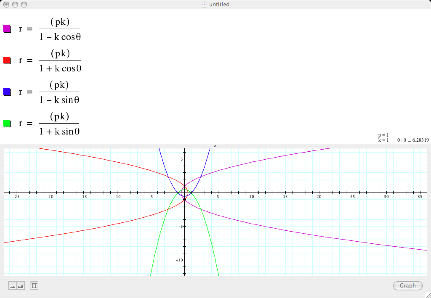
Figure 1
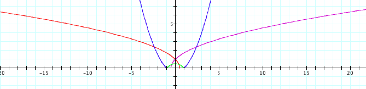
My initial graph displays a series of parabolas that all intersect with each other. The set parameters for my p-values and k-values are equal to 1. Instead of “t” as our ranging variable for rotations in parametric as we have seen before, polar equations use “theta q” as our variable. Since we are using sin and cosine functions, our values will be in terms of p. In order for our functions to graph a complete rotation and maintain their sanity, we need their parameters set from 0…2p. If not, they will only be half as sane as displayed below:
We will now conduct a psychological experiment to test how they answer a specific number of questions, called “p.” Also, we will ask the same number of questions in different ways, “k.”
As we saw in figure 1, the family has a normal response to one question. They do seem to have a distinct, yet common way of response in the shape of a parabola, illustrating the distances from the diretrix. Together, their answers generate a locus points on the conic, which will give me the information I need to determine their sanity.
Let’s explore their reaction when asked 1 question different ways.
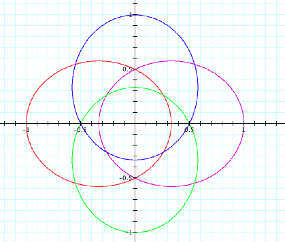
1 Question asked at .5 speed, k<1. We see here that the sin ellipse (blue and green) intersect the x-axis at 0.5 and the cosine functions intersect the x-axis at 1, which are their foci.
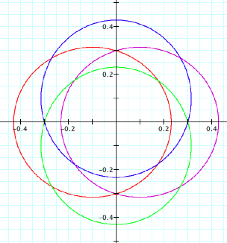
1 Question asked at .3 speed, k<1
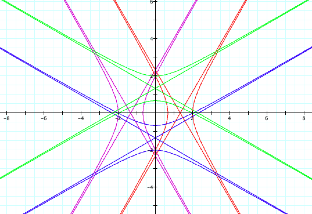
Asked 1 question twice as fast, where k=2, the family yields hyperbolic answers. Here, their focus is illustrated by their respective asymptote.
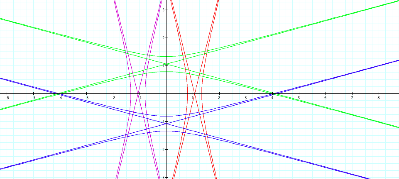
When asked 1 question 4 times as fast, where k>1.
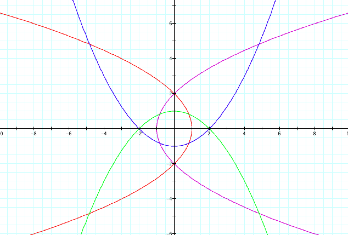
When asked 2 questions at normal speed, p =+2, the parabolas widen, yielding further foci points and directrix. This tells me that their minds are opening up and their answers are becoming more thorough.
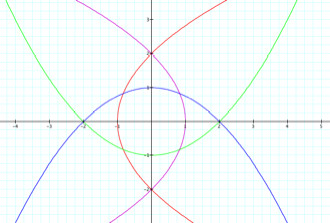
When asked 2 questions backwards at normal speed, p = -2, their total train of thought was completely reversed.
After interviewing this family my results showed that they are a normal, close-nit family, and that I am completely insane.
Return