Tangent Circles of Two Separate Circles

Brian Swanagan

 

 

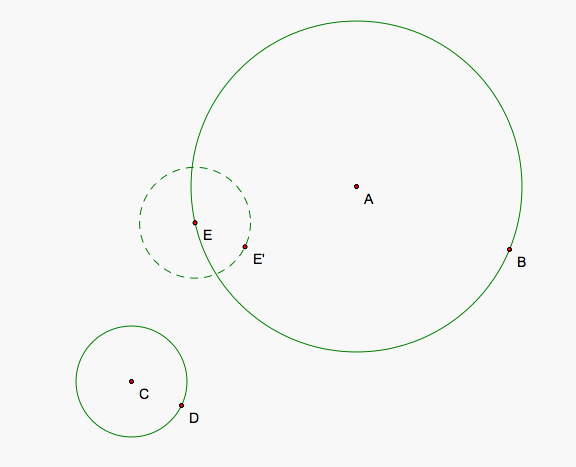
We will investigate the tangent circles to two circles that share no points within and on their boundaries. I have drawn two circles of different size below.

 

Now we choose a point E on our larger circle (or our smaller circle) and create the circle tangent the that point and tangent to the other circle. The first tangent circle I wish to create will not contain either circle so I'd like to pick a point closer to the space between them. I then draw a circle around this point E identical to the smaller circle. EE' is the same vector as CD. The tangent circle's center is lies on a line through E and A so I draw that line to give an idea of where the center could lie. We label F which is the intersection between our small circle copy and the line that lies inside the larger circle.

 

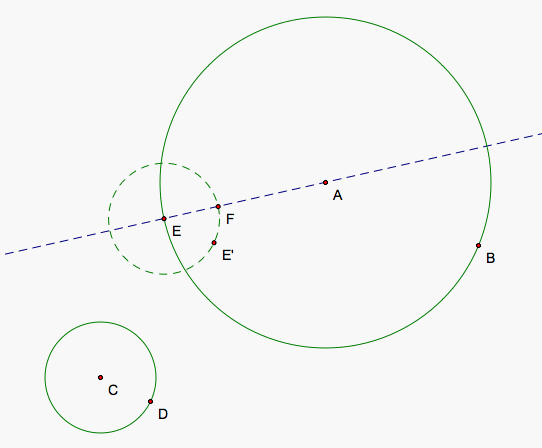
The radius of our tangent circle plus the radius of the smaller circle is the distance from the center of the smaller circle to the center of our tangent circle. The distance from the tangent circle's center from F is also the sum of the radii of the tangent and smaller circle so C, F, and the center of the tangent circle form an isosceles triangle. CF is the base of this triangle so we connect C and F with a segment and find its midpoint G. Drawing a perpendicular bisector of CF through G gives us a line that the center of the tangent circle lies on so we can find the intersection of our two lines to find the location of the center of our tangent circle. We may run into a problem when the two lines are parallel and we will discuss this case a bit later on. Now, we can draw our circle (red) since we have the center, H, and a point on the circle, E.

 

 

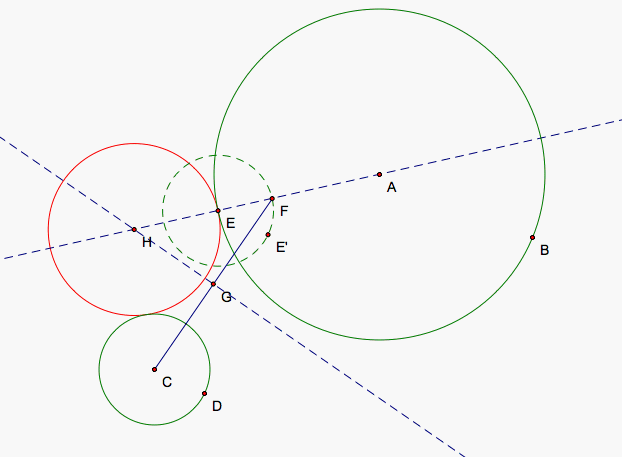
As we move farther away from the smaller circle, the tangent circle begins to increase in size and the angle HFC increases in measure

 

 

As EFC continues to increase in measure and approaches 90 degrees, the two lines begin to look more parallel so H moves quite far away from the two circles making the tangent circle enormous. We can see that it begins to look like a line itself relative to our smaller circles in the left picture. In fact, the part of the curve of the tangent circle closest to our first two circles begins to approach one of our tangent lines for our two circles. As E continues to move farther away from C, EFC becomes an obtuse angle and the center for our circle moves to the other side of our starting circles. Now, the circle is tangent to both but containes both circles. This is another set of circles tangent to our original circles a bit different from what we created originally.

 

 

 

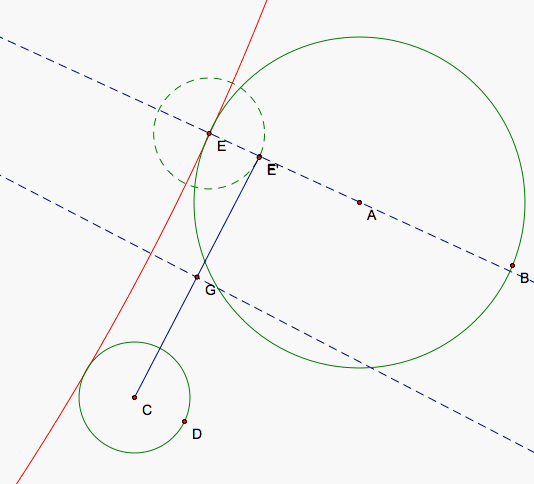
As E moves opposite to C, EFC becomes a line or a 180 degree angle and our two lines become perpendicular. H at this point has passed through one of our circles or between them. Now, our tangent circle has decreased in size as far as it can while still containing the two circles.

 

 

The tangent circle begins to grow again as E moves back around and closer to C now. EFC continues to increase in measure if we look at the larger part of the angle. At some point, EFC reaches 270 degrees and our lines become parallel again. Now the red curve of our circle approaches another tangent line of our two starting circles.

 

 

 

 

As E completes its circuit and moves closer to C, the tangent circle decreases until H lies between them both and the circle once again does not contain the two starting circles.

 

 

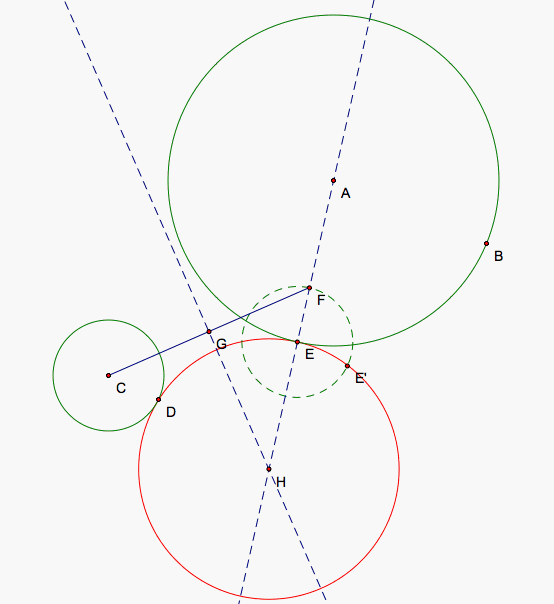
Next, we move E near its original position and begin to look more closely at the locus of center points for our tangent circles that we created during this cycle. We connect C and H with a segment first and the point I which lies on the intersection between our tangent circle and our smaller circle.

 

 

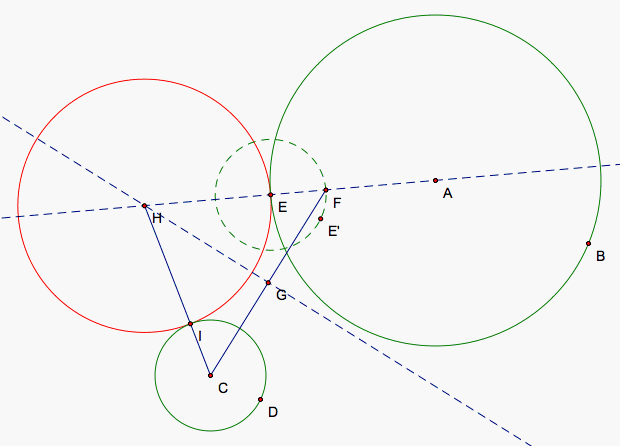
We know that HE = HI and EF = IC so HA - HC = FA which is a constant value because FA = R1 - R2 where R1 is the radius of our larger circle and R2 is the radius of our smaller circle. R1 - R2 = 0 if the two circles are the same size. That means the loci for the tangent circles that touch but do not contain the solid green circles should be a hyperbola since the distances from its center to C and A has a constant difference.

 

 

Tracing F gives us a circle around A and tracing H gives us two hyperbolic looking curves. We may wish to look more closely at the situaiton when the tangent circle encloses our two solid green circles.

 

 

 

HI = HE because they are both radii of our tangent circle. But, we know CI = FE are equal to the radius of our smaller circle. That means HC = HF and HF = HA + AF so HC - HA = AF which is again our constant difference that we found earlier. And more interestingly, HA and HC are the distances from the centers of our two circles. This means the loci of the centers of our tangent circles forms a hyperbola with the centers of our two circles as its foci whose difference from the tangent circles is always a constant distance.

 

 

 

During our last construction, we created tangent circles that either didn't enclose either of the two circles or enclosed both. We will now attempt to construct the remaining set of tangent circles that encloses exactly one of either circle. So, we construct two circles separate from each other and pic a point E on the larger of the two circles or one of the circles if they are equal. We then draw a replica of the other circle with E as its center. EE' and CD are the same vector.

 

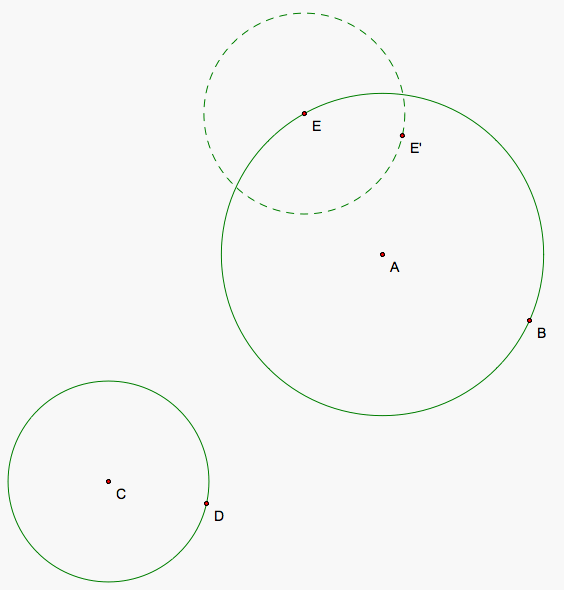
Now, we will intially attempt to create a tangent circle that encloses the larger circle but not the smaller one so we will move E so that it is not too close to C so that it has to enclose the larger circle in order to be tangent to both. The tangent circle is tangent at E so its center must lie on the line through A and E. The center of our tangent circle to E will again be equal to the distance to its tangent point on our smaller circle. The radius of our smaller circles plus the radius of the tangent circle gives us to equal distances so we need to mark the intersection of the second smaller circle and the line that is outside the larger circle. Then C, J, and the center of the tangent circle forms an isosceles triangle with CJ as its base so we connect CJ, find the segments midpoint, and draw the perpendicular bisector to CJ to give us another line that the center of the tangent circle lies on. When the two lines aren't parallel which only happens in two specific instances that we shall observe later, the intersection of the two lines gives us the center to our tangent circle that we will call L.

 

 

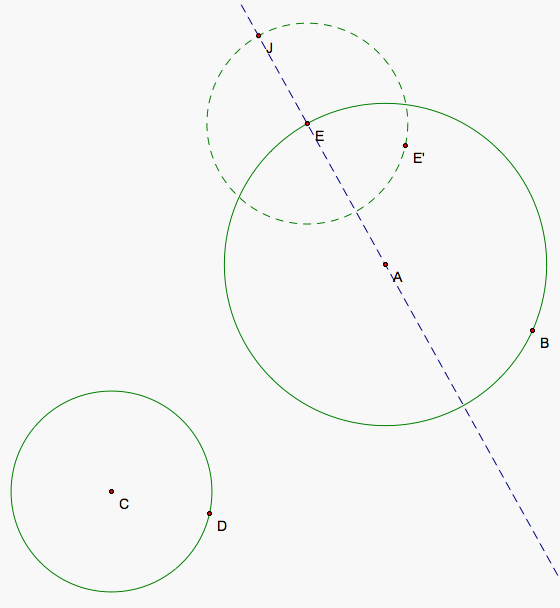
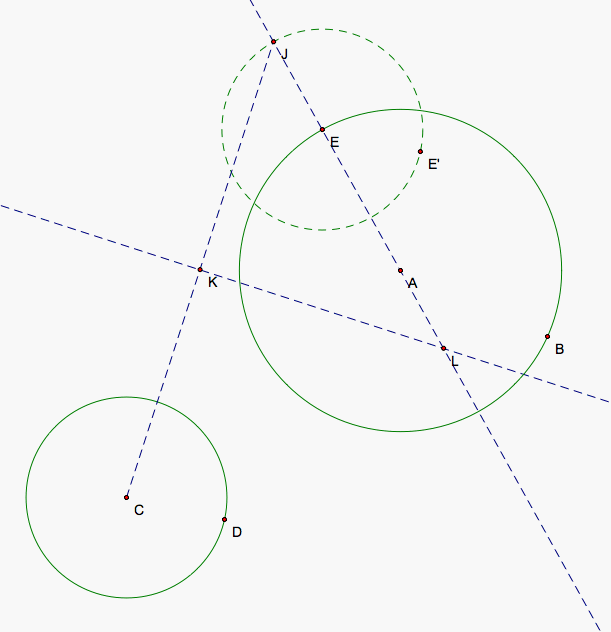
Now, we can draw our circle that passes through E and has its center at L. As E moves closer to the smaller circle, angle KJE grows as does the size of our tangent circle.

 

 

As the angle measure of KJE approaces 90 degrees, the two lines become more and more parallel and so the curve of our tangent circles approaches that of one of the tangent lines of our two circles that passes between them. As E continues to move closer to C, our tangent circle decreases in side again and now encloses only the smaller circle creating the final set of tangent circles.

 

 

 

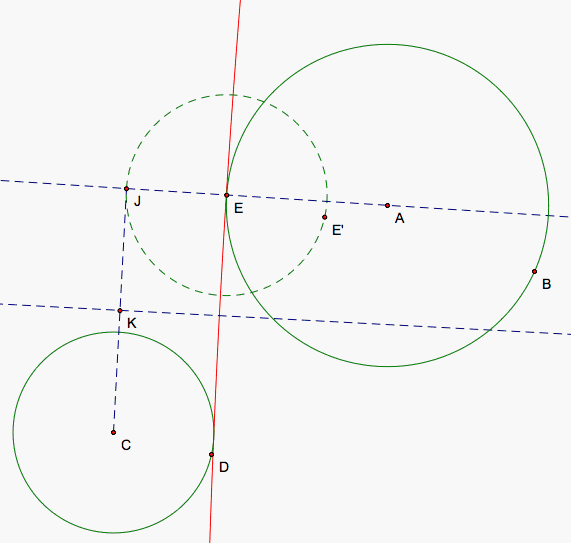
As E continues on its circuit and moves farther away from C, the tangent circle begins to increase in size again. KJE now becomes a 270 degree angle making our two lines parallel again and the curve of our tangent circle approaches the fourth and final tangent line of our circles and the second that passes between them.

 

 

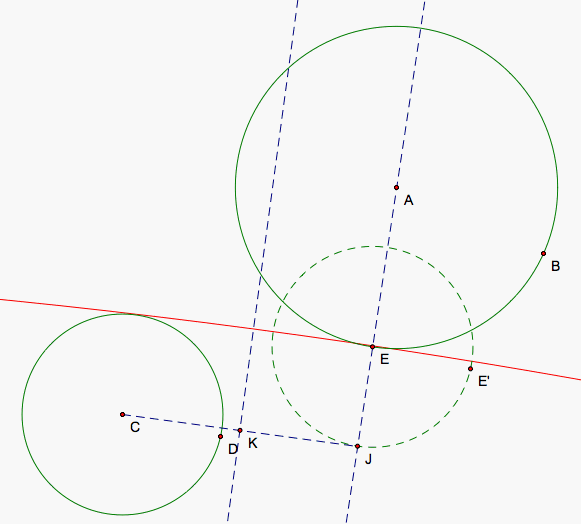
As E finishes its motion, the tangent circle now once again encloses only the larger circle completing our set of tangent circles that enclose only one of the two solid green circles.

 

 

Now, we would like to determine the nature of the loci of centers of our tangent circles that enclose exactly one of the solid green circles. LJ = CL as we said earlier because they are both the sum of the lengths of the radii of our smaller circle and our tangent circle. LJ = LA + AJ so CL - LA = AJ and AJ = R1 + R2 where R1 and R2 are the lengths of the radii of our larger and smaller circles, respectively. So, again we have the difference of the distances from the centers of our green circles to the tangent circle is a constant once more which should give a hyperbolic curve.

 

 

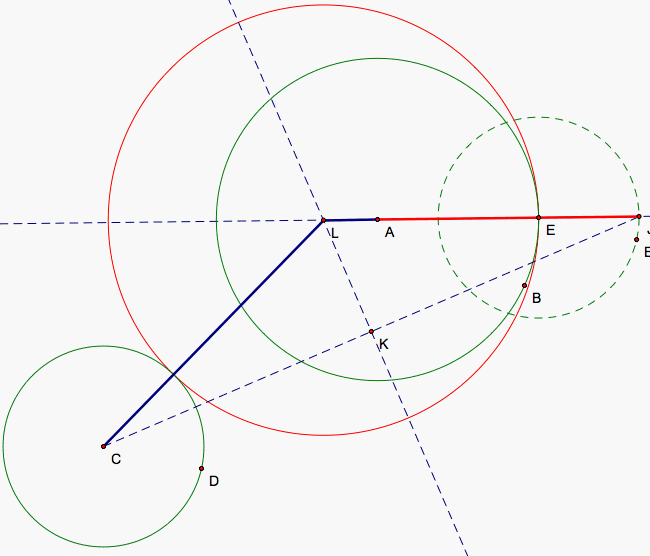
:Let's make sure our curve is still hyperbolic in nature when the tangent circle only encloses the smaller circle. Again, CL = LJ because CL plus the radius of our smaller circle and LJ + EJ (the radius of our smaller circle) are both the radius of our tangent circle. LA = AJ + LJ and CL = LJ so LA - CL = AJ our constant difference once again.

 

 

In both cases, the difference of the distances from the centers of our solid green circles to the center of our tangent circle is always constant so we have a hyperbolic curve if we trace the center, L, of our tangent circle (traced in black). We should also have a circle if we trace our constant lengthed segment AJ (traced in red). Indeed, we see that this is the case.

 

 

This means that the loci of the centers of the tangent circles for two separate circles is hypberolic with the foci at the center of our two separate circles.