Orthocenter Equations

Brian Swanagan

 

 

 

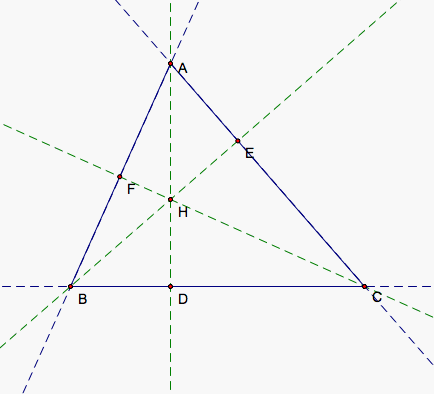
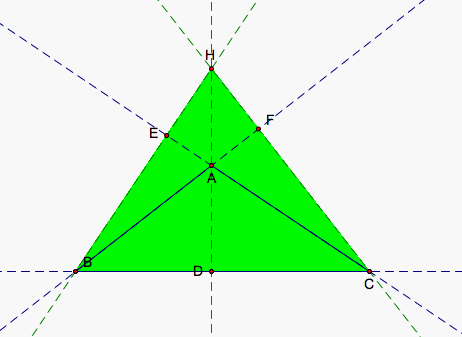
Suppose we have an acute triangle ABC like the one above. We can draw lines through each vertex perpendicular to the side opposite it. D, E, and F are the resulting intersections for a line through each side and the line perpendicular to it. H is the intersection of all three perpendicular lines. Then AD, BE, and CF are all altitudes for our triangle. We would like to prove the following equations.

 

 

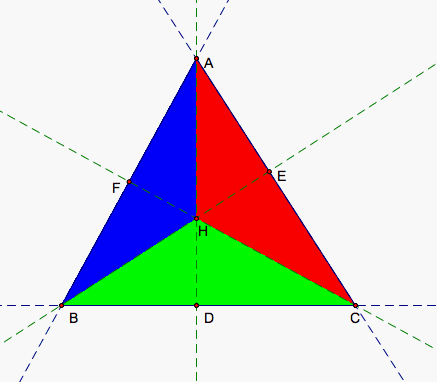
We will start with the top equation, referred to from now on as Equation 1. The bottom equation will be referred to as Equation 2. Suppose we multiply the top and bottom of the first fraction in Equation 1 by 1/2*BC. Then 1/2*HD*BC gives us the area of the green triangle depicted below in the next picture and 1/2*AD*BC gives us the area of our entire triangle. Similarly, we could multiply the top and bottom of the second fraction by 1/2*CA and the top and bottom of the third fraction by 1/2*AB. Then, 1/2*HE*CA gives us the area of our red triangle shown below, 1/2*HF*AB gives us the area of our blue triangle displayed below, and both 1/2*BE*CA and 1/2*CF*AB give us the area of our entire triangle. So, 1/2*AD*BC = 1/2*BE*CA = 1/2*CF*AB.

Now, our expression for the left-hand side of Equation 1 (let's call it Expression 1) can be simplified to (1/2*HD*BC + 1/2*HE*CA + 1/2*HF*AB)/(1/2*AD*BC). Moreover, the sum of the area of the green, red, and blue triangles is the same as the entire triangle. Then, our expression can be simplified to (1/2*AD*BC)/(1/2*AD*BC) = 1 as we wanted. Equation 1 then is true for acute triangles since the same demonstration can be made for each.

We also can see that AD = AH + HD, BE = BH + HE, CF = CH + HF so AH = AD - HD, BH = BE -HE, CH = CF - HF. Our expression for the left-hand side of Equation 2 (let's call it Expression 2) can be altered by substituting these known equalities to become (AD - HD)/AD + (BE - HE)/BE + (CF - HF)/CF = AD/AD + BE/BE + CF/CF - (HD/AD + HE/BE + HF/CF) = 3 - (HD/AD + HE/BE + HF/CF). We can substitute our result from the first equation so that our expression equals 3 - 1 = 2 just as we wanted as well. Equation 2 is also true for acute triangles then. Indeed, Equation 1 being true implies Equation 2 is true through the same argument used here so for future triangles we need only show Equation 1 is true.

 

 

 

Suppose instead taht ABC is a right triangle. If the right angle is at B, then HD = HF = 0 and HE = BE while AD and CF are nonzero so that (Expression 1) = 0 + 1 + 0 = 1. If the right angle is at C, then HD = HE = 0 and HF = CF while AD and BE are nonzero giving us 0+0+1 = 1 for Expression 1 again. And finally if the right angle is at A, then HE = HF = 0 and HD = AD while BE and CF are nonzero so (Expression 1) = 1 + 0 + 0 = 1.

 

 

 

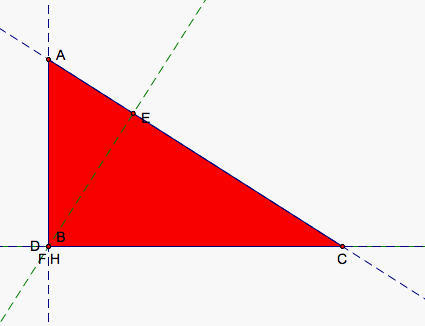
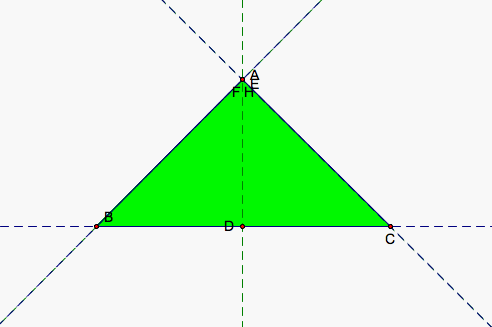
Now, we would like to show Equation 1 holds for obtuse triangle if indeed it does hold. If we take only positive distances HD, HE, and HF, then it is quite easy to demonstrate by example that our equations do not hold. But, if instead we say that some of our segments change orientation as H passes through a vertex of our triangle, then the equations might still hold. Certainly if A does not cross the line through B and C, our original triangle maintains the same orientation and AD, BE, and CF all remain positive. When H lies outside the triangle, then AH or HD and BH or HE and CH or HF is greater in magnitude than AD, BE, and CF respectively so one of each of the pairs must be negative in order for AD = AH + HD, BE = BH + BE, and CF = CH + HF to continue to hold.

Suppose we orient our segments HD, HE, and HF according to the orientation of the triangle that we associated them with above. So, if HBC is negatively oriented then and only then HD is negative because its area is 1/2*HD*BC and BC hasn't moved. Similarly while A remains above the line through BC, AB and CA are positively oriented so if HCA is negatively oriented then and only then HE is negative and if HAB is negatively oriented then and only then HF is negative.

 

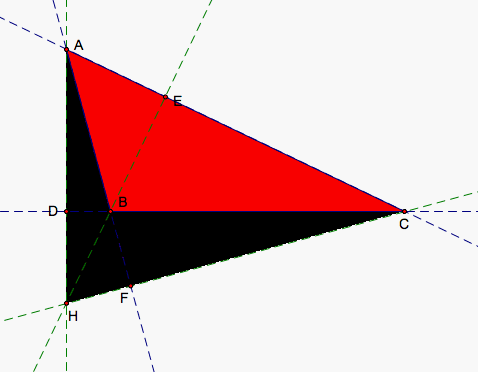
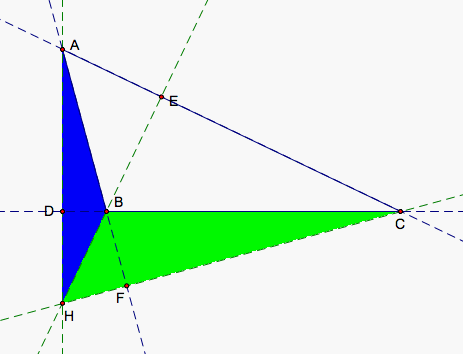
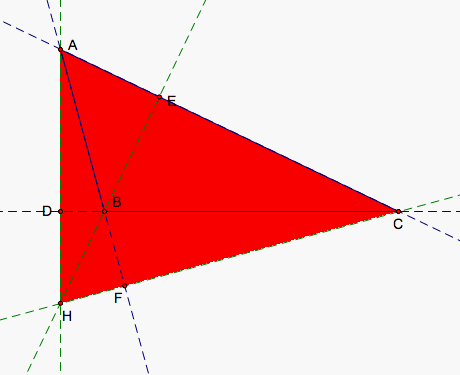
If we move A to make B obtuse, then H passes through B causing the orientation of two triangles to change. HBC and HAB now go clockwise so the orientation of those two trianges is negative. HCA and ABC remain positive. We can see in our first picture that we have can see a triangle that is both black and red. The black area is area made up of two of our triangles, red and blue or red and green. The red triangle HCA (shown in the third picture) actually is the larger of our triangles at the moment and the negatively oriented triangles HAB and HBC (showin in the second picture) subtract from our red triangle to give us ABC.

So, HD/AD + HE/BE + HF/CF = (1/2*HD*BC)/(1/2*AD*BC) + (1/2*HE*CA)/(1/2*BE*CA) + (1/2*HF*AB)/(1/2*CF*AB) = (1/2*HD*BC + 1/2*HE*CA + 1/2*HF*AB)/(1/2*AD*BC) = (Area of ABC)/(Area of ABC) = 1 yet again. Then, our red, blue, and green triangles still add to make our triangle ABC except that now the red triangle contains ABC and the blue and green triangles make up the region of the red triangle that is not included in ABC. Equation 1 still holds.

 

 

 

If we move A so that C is obtuse, we run into a similar situation. The blue triangle now contains ABC and the green and red triangles who are now negatively oriented make up the region of our blue triangle HAB that does not lie within ABC. Using the same reasoning for when B is obtuse, we quickly find that Equation 1 continues to hold.

 

 

 

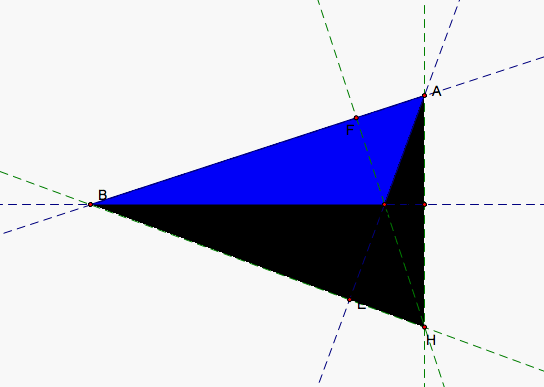
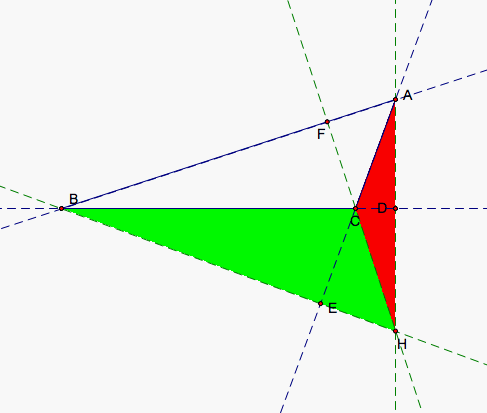
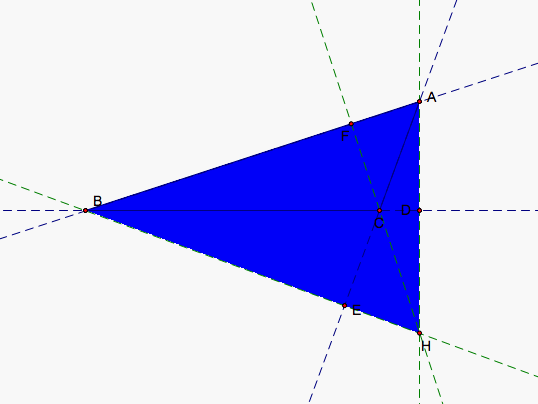
The final situation is when A is obtuse. Yet again, we have one of our colored triangles, green HBC this time, that contains ABC and the other two triangles, red and blue, that make up the area within the larger triangle that does not lie in ABC. So, the summation of the three colored areas gives the area of ABC allowing Equation 1 to hold.

 

 

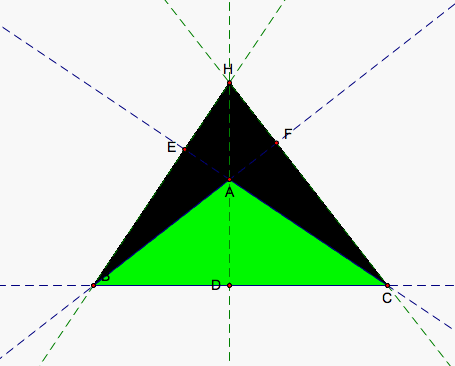
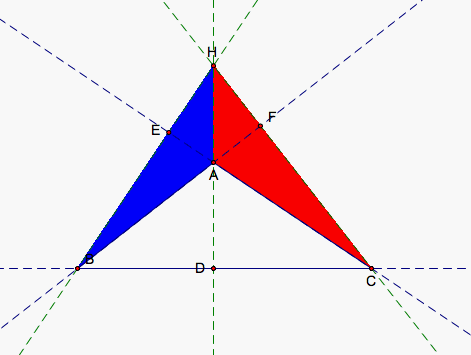
When A crosses the line through BC, the resulting set of triangles are just reflections of the triangles we have determined here. So, ABC changes orientation as do all our smaller triangles. So, AH, HD, BH, HE, CH, HF, AD, DE, and CF all change sign. Because both the top and bottoms of all our fractions in our two equations change sign, the sign of the fractions do not change giving us the same result as before.

So, Equation 1 holds for all triangles. From earlier, we determined from our interpretations that 3 - (Expression 1) = Expression 2 and (Expression 1) = 1 for all triangles so 3 - 1 = 2 = (Expression 2) for all triangles. Then Equation 2 also holds for all triangles.