A Linear Intersection of Circles

Brian Swanagan

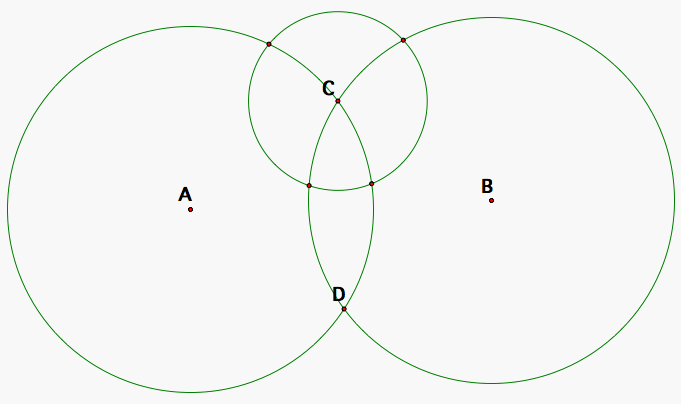
Suppose we have two intersecting circles with the same radius centered at A and B that intersect at exactly two distinct points C and D as well as a circle centered at C that intersects circles A and B (by circle A, I mean the circle centered at A and will do similarly for the other circles). We would like to prove that one intersection of circle A with circle C and one intersection of circle B with circle C are colinear with intersection D of the two circles A and B.

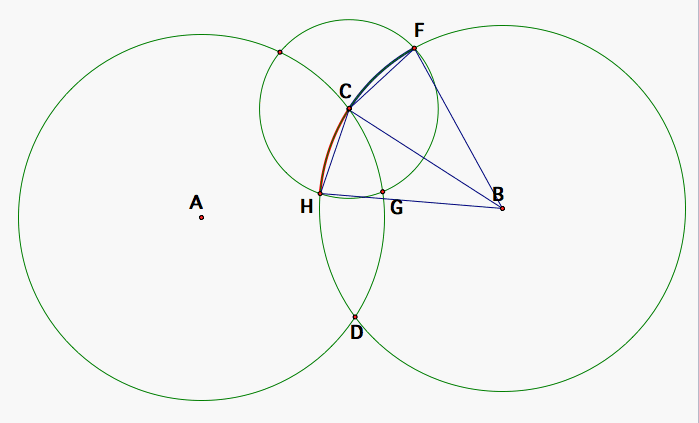
Let's name the points of intersection by circle C with circles A and B that will be of interest to us: F, G, and H as shown in the diagram. But in case the images aren't coming up, F is the intersection of circle C with circle B that is clockwise from point C, G is the intersection of circle C with circle A that is clockwise from point C, and H is the intersection of circle C with circle B that is counterclockwise from point C.

First, we will consider the case where H is within circle A and G is within circle B (in otherwords, the radius of circle C is not longer than the segment CD).

We know that if we create segments from C to F, G, and H then they will have equal length since they are all radii of circle C.

Let's also draw the segment from C to D.

Now for a moment, let's remove segments CD and CG, briefly but keep them in mind. CF and CH are segments of equal length as we said before and we also know that BF, BC, and BH are segments of equal length because they are all radii of circle B. Then triangles FBC and CBHare congruent by the SSS Triangle Congruency Theorem. That means that angles <FBC and <CBH are congruent as well since they are corresponding angles of two congruent triangles. The arcs FC and CH then are equal because they are both subtended by congruent central angles.

Now, let's put back segment CD and add segments HD and FD. <CDH and <FDC subtend arcs of equal measure so by the Arc Angle Theorem, they are both half the angle measure of the central angle that subtends those two arcs making <CDH and <FDC congruent as well.

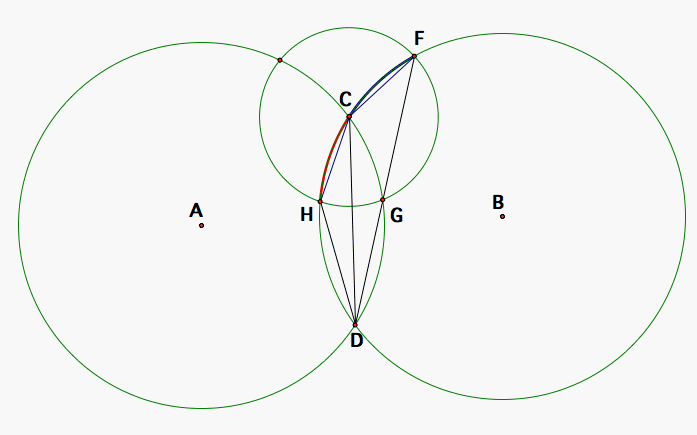
Now, we don't know that FD passes through G so I take it away so that you can simply visualize for a moment that it may not pass through G but only happens to be very close to that intersection.

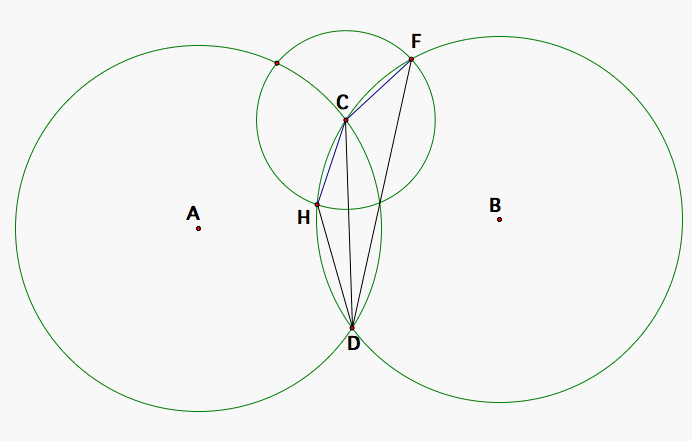
So, now let's look at the congruent segments CH and CG without CF, DC, DF, and DH. Segments AC and AG are congruent because they are radii of circle A and, furthermore, are congruent to segments BC and BH (radii of circle B) because we stated earlier that the two circles, A and B, had the same radius. Then, triangles GAC and CBH are congruent by the SSS Triangle Congruency Theorem. So, <GAC and <CBH are congruent angles because they are corresponding angles of two congruent triangles. Since they are equal in measure, they subtend arcs of the same radial measure, GC and CH.

Now, let's bring back segments CD and DH and draw segment DG. <CDH and <GDC subtend arcs of the same radial measure so they are both half the angle of the equal central angles that subtend those arcs by the Arc Angle Theorem so <CDH and <GDC are congruent to each other in angle measure.

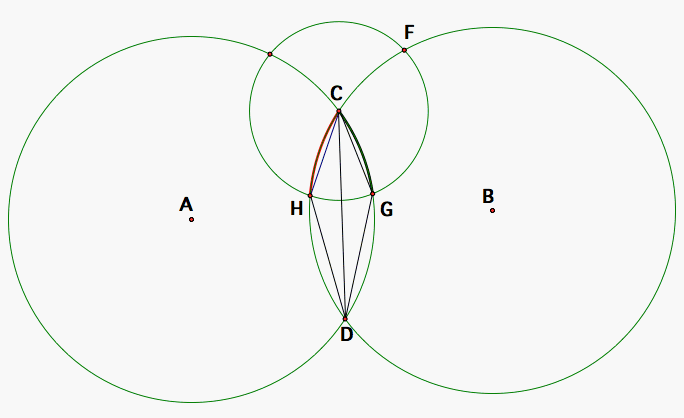
So, now we know that <CDH is congruent to <GDC. But, keep in mind that the line through DG may not pass through F and may only get really close.

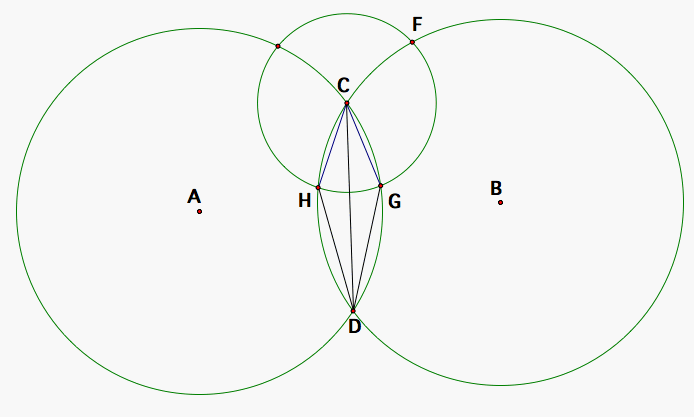
So, lets look now at the circles with segments DC, CG, CF, DG, and DF. We know that <FDC is congruent to <CDH and that <CDH is congruent to <GDC so by the Transitive Property, we have that <FDC is congruent to <GDC. Since G may only be very close to the segment DF, we should consider the angle <FDG that would then be positive (or negative if the angle orientation is clockwise due to G being on one side or the other of segment DF). So, <FDC is the sum of the angles <FDG and <GDC. But, we know that <FDC and <GDC are equal in measure. That means that <FDG is 0 in angle measure which implies that F lies on ray DG a subset of the line through DG.

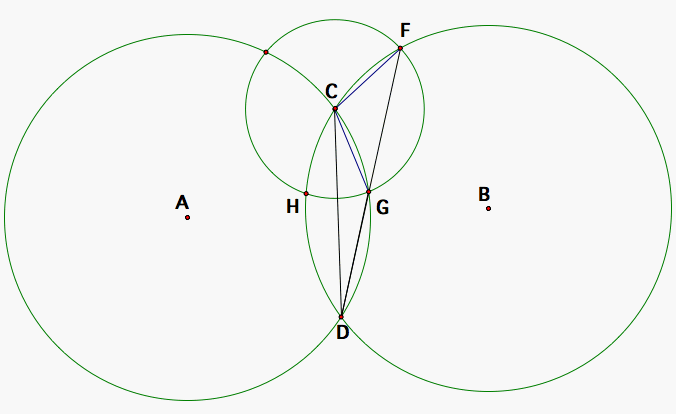
Therefore, D, G, and F are colinear.

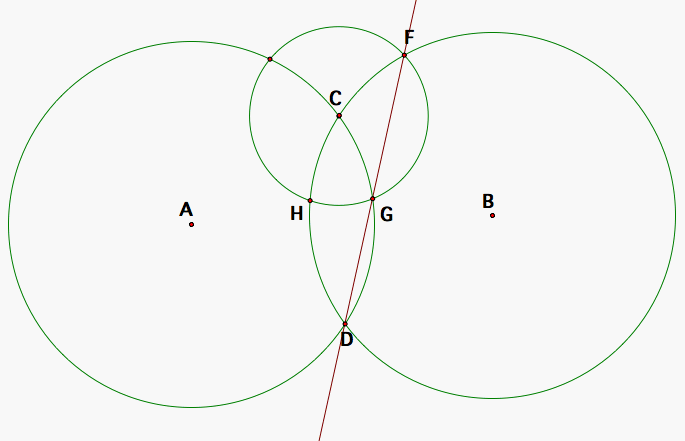
The second case is where G does not lie within circle B and H does not lie within circle A. We will take it to be true that on circles of equal radius, arcs of equal length chords will also be equal following the proofs we did earlier in the first case.

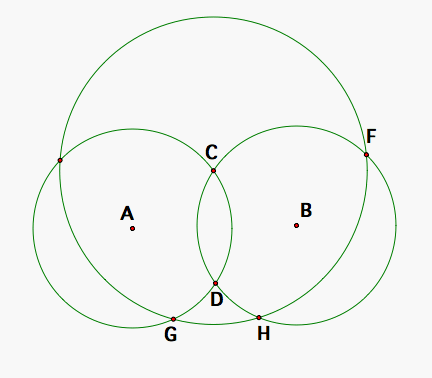
Let's draw segments FC and CH which are both radii of circle C so they are congruent. Then the arc FC (I will assume counterclockwise from F to C when I state arcs which is what I also assumed earlier) is congruent to arc CH. <FDC subtends arc FC and <HDC subtends arc HC which is the complement of arc CH on circle B. Then measure of arc FC which is congruent to CH and the measure of arc HC together are 360 degrees. Then, the sum of the measures of <FDC and <HDC is 180 degrees since they are half the measure of each of those two arcs by the Arc Angle Theorem.

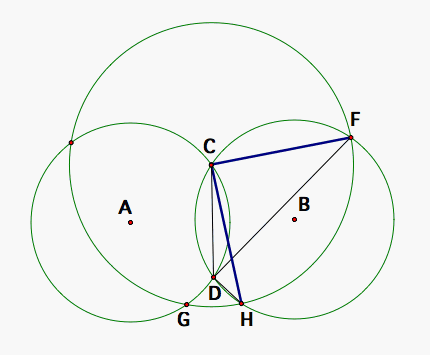
Now, let's look at segments CH and GC. They are both radii of circle C so they are congruent. Circle A and circle B are congruent circles so arcs HC and CH are congruent which means that <HDC and <CDG which subtend these arcs, respectively, are equal in measure.

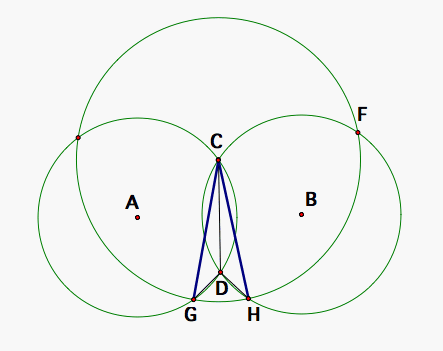
Then the measure of <FDC, which is the sum of <FDC and <CDF, is also the sum of their measures which is equal to the sum of the measures of <FDC and <HDC since <HDC is congruent to <CDG. So, <FDC is 180 degrees.

That implies that F, D, and G are colinear!

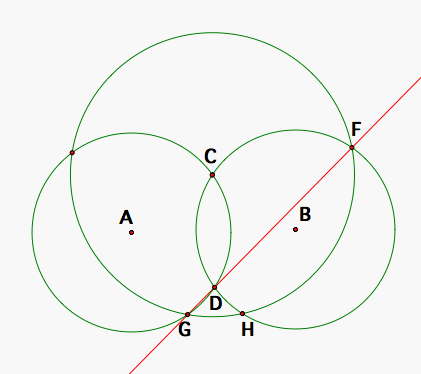
This also works for when F and H become one one point as the radius of circle C becomes the length of the diameters of circles A and B (after which there is no longer any intersections between circle C and the two others). But, we can prove this also a bit more simply using the fact that CF and CG are the diameters of circle B and A, respectively.

Both arcs of CF and of CG are half the circle so any angle subtending them is 90 degrees. That means that <FDC and <CDG are both right angles and are therefore supplementary which means that <HDG, the sum of those two angles, is 180 degrees.

That means H, D, and G are colinear!