

In this exploration will look orthocenters of different triangles. We will start by construction any triangle ABC and then
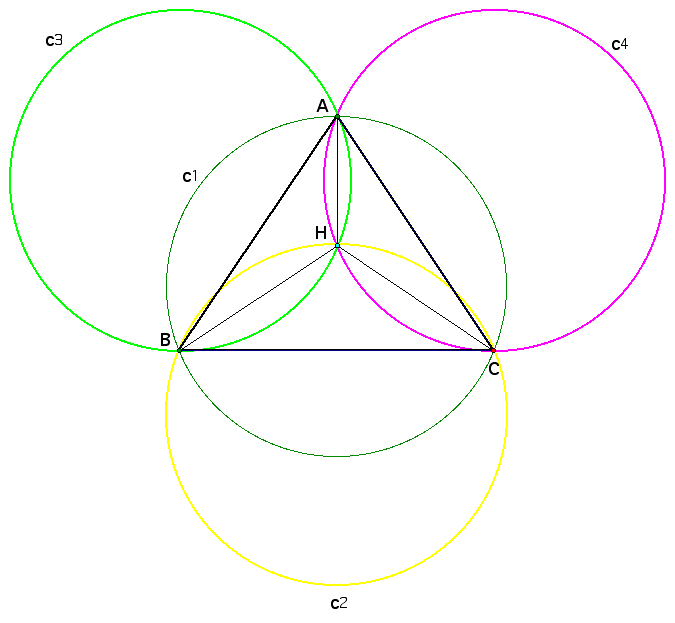
So, each vertex of the triangle ABC is the orthocenter of other triangles constructed by the orthocenter of ABC. In other words, the orthocenter of HBC is vertex A, the orthocenter of HAB is vertex C, and the orthocenter of HAC is vertex B. Also from this construction, we know that the radius are the same for each of the triangles ABC, ABH, BCH, and CAH.
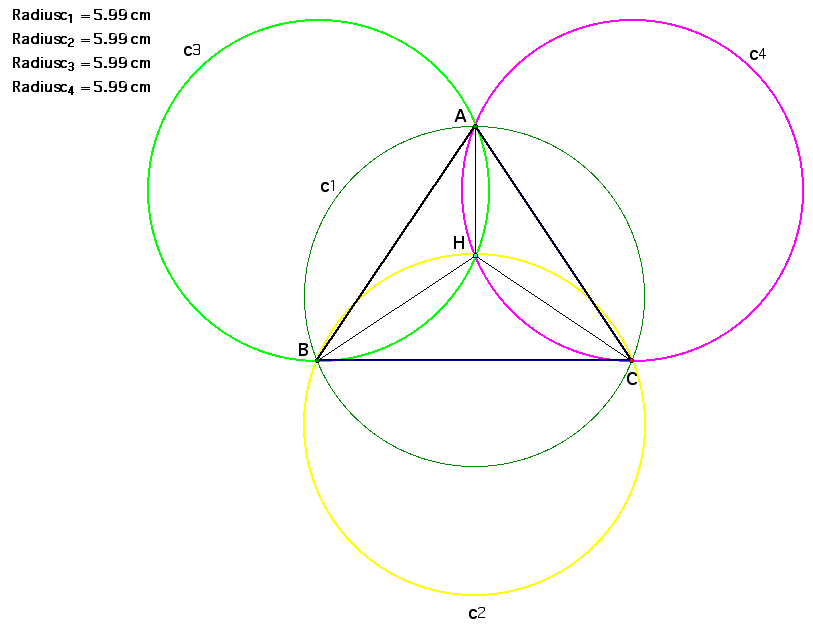
In addition, the area of ABC and the area of the triangle formed from the three centers are the same. They are also congruent to each other!
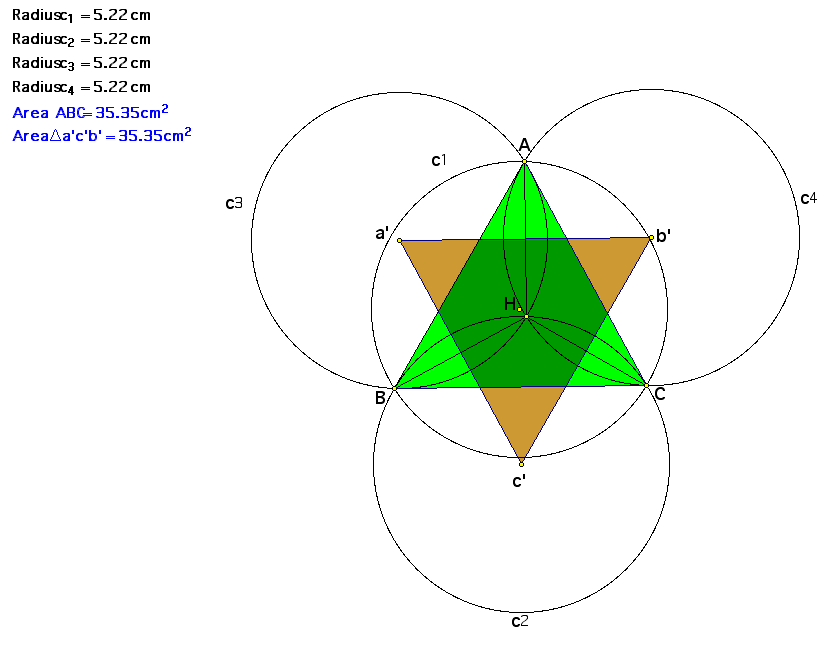
So we see that a'b' is parallel to BC, a'c' is parallel to AC, and b'c' is parallel to AB. Now, from the GSP file, we can see that the orthocenter goes on the outside of triangle ABC. Click HERE to Play with the file!