
Investigation on Polar Equations
by
Larousse Charlot
To have polar equations, one needs polar coordinates. The polar coordinates are in the form
of parametric equations.
For instance,
x = r cos q
y = r sin q
At times, one might have coordinates, but not polar
coordinates. So, the need to know
how to acquire polar coordinate is rather essential.
Obtaining Polar coordinates
Let us say we are given rectangular coordinates such as
(1,1), how does one go about converting that into polar coordinates. Since, the polar coordinates are in the
form of polar function, let us use a circle on the Descartes plane to help us
geometrically.
The reason for polar coordinates is that circle does not
quite translate well in x-y coordinate system, rectangular coordinates. The alternative description involves of
specifying the distance form the origin and the angle measure the positive
x-axis counterclockwise to the ray connecting the point and the origin. For example,

rectangular coordinates
Polar coordinates, on the other hand, indicate the distance and the angle. For, if speaking of circle, we must have angle.

polar coordinates
In polar coordinates, to find the angle q, by the definition of sine function, we have

hence, the angle

If given a rectangular coordinate (3, 4), we now can convert
that into polar coordinates.
Since r is the distance from the origin to the coordinate,

in this case,
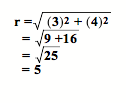
and now to find q,

Now, we can talk about polar equations. A polar equation is
in the form of r = f(q). r = f(q) is the set of all points (x,y)
for which x = r cos q ,y = sin q and r = f(q). The graph of a polar equation is a
graph in the Descartes plane of all those points whose polar coordinates
satisfy the given equation.
Let us investigate r = a + b cos (kq).
If we graph this,

a = b = k 1 0
£ q £ 2p
we get a cardiod. A cardiod is of the class of lamiVon, which is defined by the equation of
r = a ± b sin q and r = a ± b cos q. A cardiod is a lamiVon with the constants a = b.
When the constant k alters, we have

a = b purple:
k = 2 red: k = 3 blue: k = 4 green: k = 5 0
£ q £ 2p
an n-leaf rose.
What we observe here is that the value of k indicates the number of leaf
rose in the graph. What happens to
the graph as k approaches infinity?
Now, if we have the equation
r = b cos (kq)
would you say that this equation is of the class of lamiVon? The answer is yes; find why.
If compare the graphs of the two equations,

a = b = 1 k
= 2 0 £ q £ 2p
we have to cardiods, one of which is four leaf rose. What we see here, is that with the
equation
r = b cos(kq) the number of leafs is twice
the value of k. But wait, what
happens when k = 3?

a = b = 1 k
= 3 0 £ q £ 2p
Oh my! Our hypothesis does not hold. For when k = 3, we only have a three
leaf rose. Observe the following
graphs.

purple & red: k = 3 blue:
k = 4 0
£ q £ 2p
Here, we observe that when k is odd the amount of leaf
equals to k, and when k is even the number of leaf is 2k. Well, is this observation true for all
k?

purple & red: k = 3 blue:
k = 4 green:
k = 5 black:
k = 6
With the observation of this graph here, our theory
holds. For the equation r = b cos
(kq),
when k is odd the number of leaf equals to k, and k is even the number of leaf
is 2k, for any integer k ë Z.
Using your conclusion, what would happen if the equations
were to be in sine instead of cosine?
Well, IÕll tell you that our theory holds still. The graph would only change to fit the
definition of sine functions. Find out the reason. Play with the
graphs