
Exploration of Altitudes and Orthocenters
by
Larousse Charlot
Suppose we have a triangle D ABC
To find the orthocenter of this triangle, we find the perpendicular lines of the segment that pass through each opposite vertex.
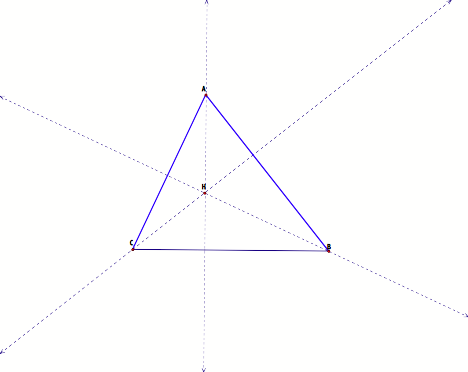
The intersection point H of the perpendicular lines is the orthocenter of the triangle DABC.
With the orthocenter, we have three additional triangles, DHBC, DHAB, and DHAC.
When construct the orthocenters of these triangles, what we find is that the orthocenters for these triangles are already there on the figure.
Observe.
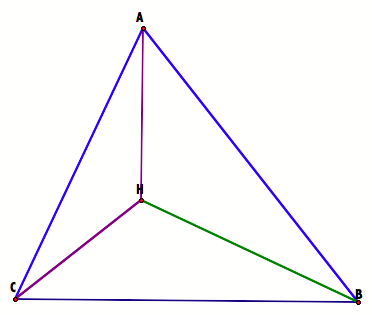
The orthocenter of DHBC is A; the orthocenter of DHBA is C; the orthocenter of DHAC is B.
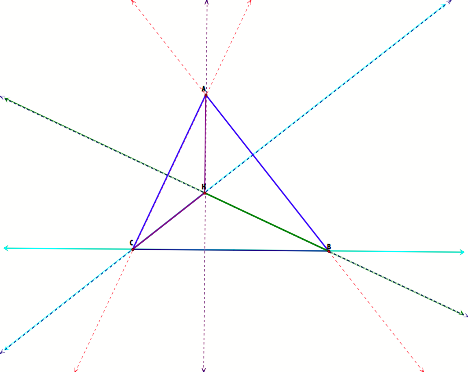
With this observation, we can conclude that similar action will happen for the altitudes of the triangles. We can construct the altitudes of the triangles as follow
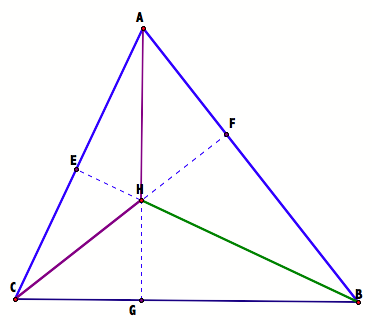
The Altitudes:
DABC has the altitudes of AG, BE, and CF
DHBC has the altitudes of HG, EC, and FB
DHBA has the altitudes of HF, AE, and BG
DHAC has the altitudes of EH, AF, and CG
These segments were not just constructed; they are part of lines through which we build the orthocenter H and the segments of DABC. Behold.
So, if the orthocenter of the DABC were to be relocated at any vertex of the triangle, the vertex would be the orthocenter of the new triangle, and that triangle should be one of the three triangles previously mentioned. See it here
When the nine points circles of each of the four triangles was built, all the triangles have the same nine points circle.
Given that the nine point circle intersect the midpoint of every segments, including the segments from the vertices to the orthocenter of the triangle, all the triangles share the midpoints of the segments. Since, the nine points circle passes through all the midpoints, and the triangles share all the midpoints, they must share the same nine points circle that passes through those shared points.