For this investigation we are going to look at the equation
while b is varied and the variables a and c are held constant. So let's start with the graph where all variables, a, b and c, are equal to 1.
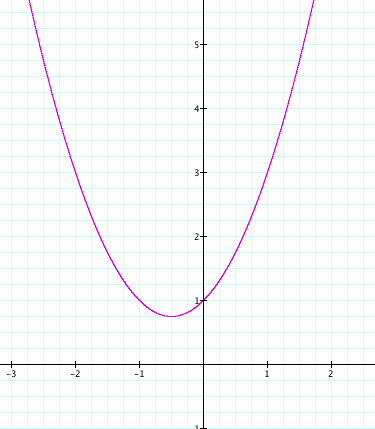
The graph opens upward because a is postive. If a was negative the graph would open in the negative direcction. It is not symmetrical around the y-axis because c = 1. Because c = 1, when x = 0, the parabola passes through the point (0, 1). If c equaled 0, then the parabola would be symmetrical around the y-axis.
Now let's look at what happens when we change b, while a and c remain 1.
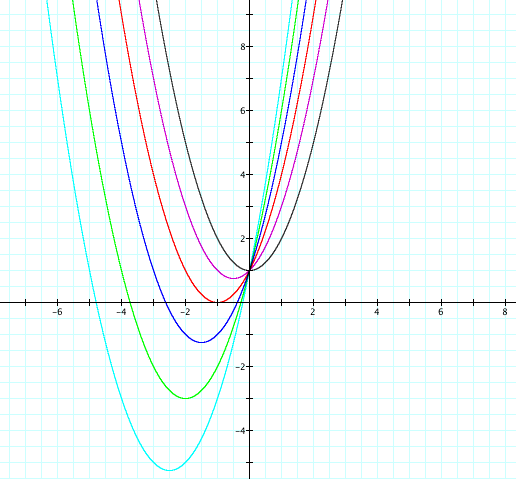
For these positive values of b, the graph always intersects the y-axis at the point (0, 1). The vertex is always to the left of the graph when b > 0. When b = 0, the vertex is on the y-axis. We know that where the parabola intersects or hits the x-axis is where the real roots of that particular equation occur. For those graphs that do not intersect or hit the x-axis, then they do not have any real roots. For example, when b = 1, the graph does not hit the x-axis, therefore it does not have any real roots. Notice that when tb is positive, the real roots occur on the negative side of the y-axis.
Now let's see what happens when b is negative.
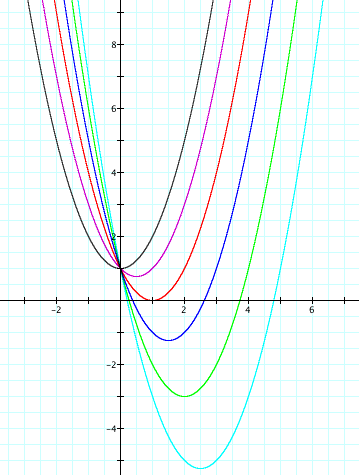
For these negative values of b, the graph always intersects the y-axis at the point (0, 1). The vertex is always to the right of the graph when b > 0. When b = 0, the vertex is on the y-axis. We know that where the parabola intersects or hits the x-axis is where the real roots of that particular equation occur. For those graphs that do not intersect or hit the x-axis, then they do not have any real roots. For example, when b = -1, the graph does not hit the x-axis, therefore it does not have any real roots. Notice that all the real roots when b is negative occur on the positive side of the y-axis.
Now let's take a closer look
at the actual vertices of the parabolas. What would happen if
we just graphed the vertices of the parabolas we have just graphed.
Where would its vertice be? Wherever the vertice was would be
known as the locus of vertices. By looking at the above graphs,
we can see that the vertices are continually going further below
the x-axis and and further away from the y-axis. That tells me
that the parabola is facing down in the negative direction, therefore
the 
term is negative. We can see that
all the vertices are steadily climbing towards the point (0, 1),
then the c for the equation must be 1. And since the vertex is
on the y-axis, we know that b = 0. Therefore the equation must
be 
. Now lets graph the locus of vertices
equation along with our other equations.
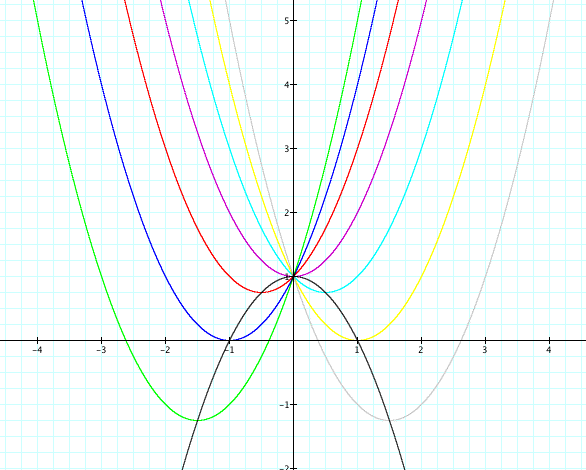
We can see that the locus of vertices parabola passes through the vertices of the of all the other parabolas. We can see that all the c's are the same and that the locus of vertices has the opposite a of the other equations. And we notice that yes, b does in fact equal 0. But how do we know that it will work for all equations?
Let's plug in some different a's and c's to check to make sure. How about a = 2 and c = 3.
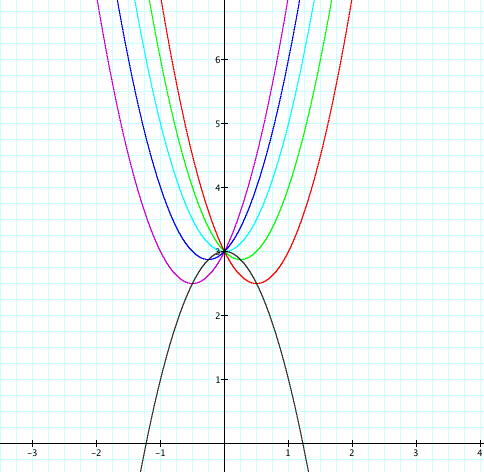
We can see that the same thing happens as before. But does the same thing happen if a is negative to begin with. Let's let a = -3 and c = -2.
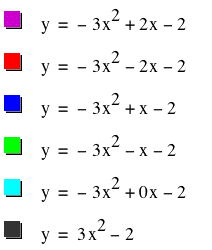
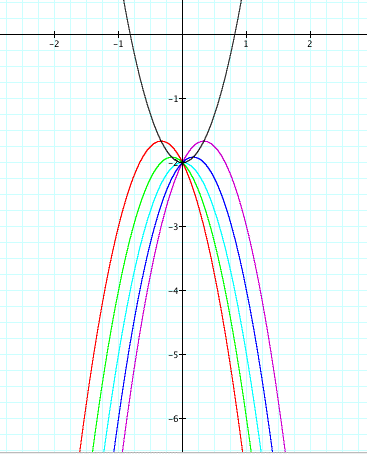
Once again the locus of vertices passes through all the vertices of the parabola. Therefore we may assume that the locus of vertices equation would be equal to the opposite of a plus or minus c. Therefore if a was positive and c was positive, then the locus of vertices would be
and
if a was negative and c was negative then, 
.
And if a was positive and c was negative, then 
and
if a was negative and c was positive, then 
.
By Carolyn Amos