

Given line segments j, k and m. If these are the medians of a triangle, construct the triangle.
First I had to build the triangle using the medians I had been given, so I placed the three medians together to create a triangle.
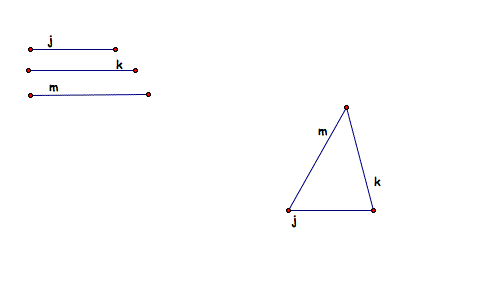
The next thing I did was make the centroid of the triangle, by finding the midpoints of the medians and then connecting a vertex with the midpoint of the opposite side. Then I drew a line along the median from that vertex used in the circle, and found the intersection, A, of that line and the circle. Where the line intersects the circle you have drawn, will be the midpoint of the sides of the triangle.
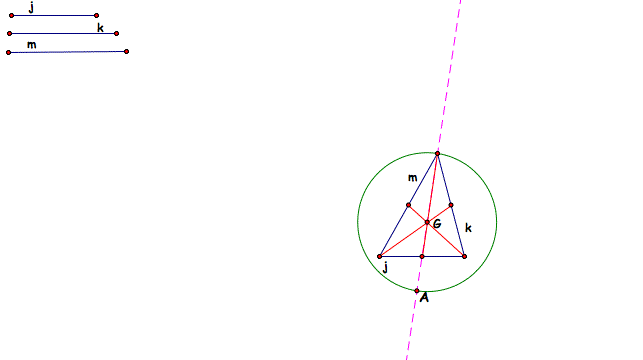
Now we can let C1 (the intersection of median j and median k) be a vertex of our triangle we are creating. Now make a circle with center A (the midpoint of one of the sides of the triangle) and radius C1.
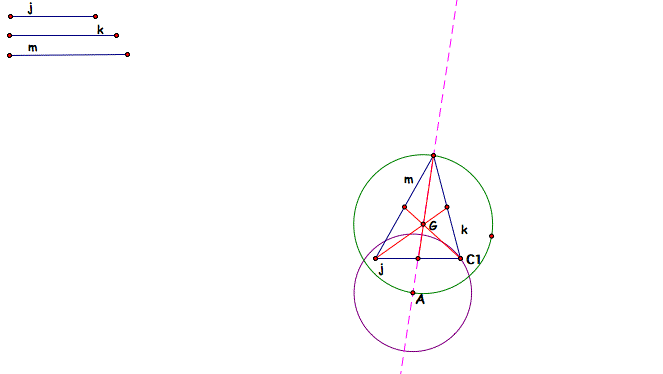
Now draw a line through C1 and A and create the point C2 at the intersection of the line and the circle. Point A is the center of the circle and the radius goes from A to C1 and another radius exists from A to C2. Since we know that all radii on a circle are equal, A is the midpoint of segment between C1 and C2. This means that the segment is one side of the triangle we are looking for. So connect the segment to make the first side of the triangle.
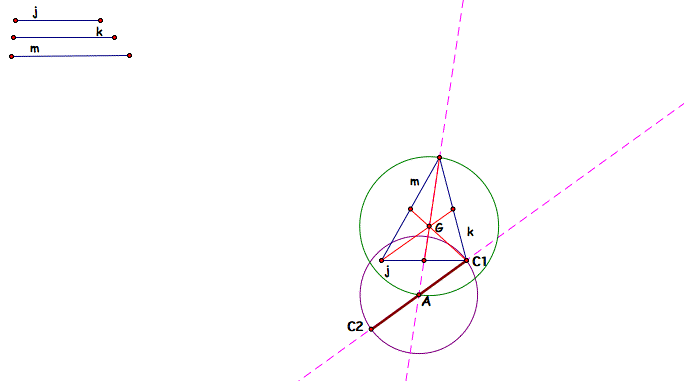
Now we need to create another side from C1 to what will be C3. We know that the length of the median is 3/4 of the length of the side that we need. So we need to constrct another circle with the midpoint of median m as the center and radius to G. Then we need to create a line through the circle along the radius from G through the center.
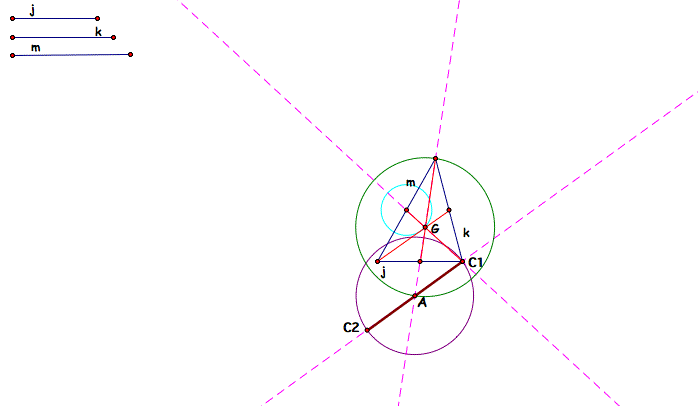
The point where that line intersects with the circle of radius G is labeled C3 and is the third vertex of our triangle. So we connect C1 and C3 to find the second side of our triangle. Then all we need to do is connect C2 and C3 to make the last side of out triangle. The segment connecting the last side of the triangle should pass through the intersection of medians j and m. Now we can see our triangle fully outlined in brown.
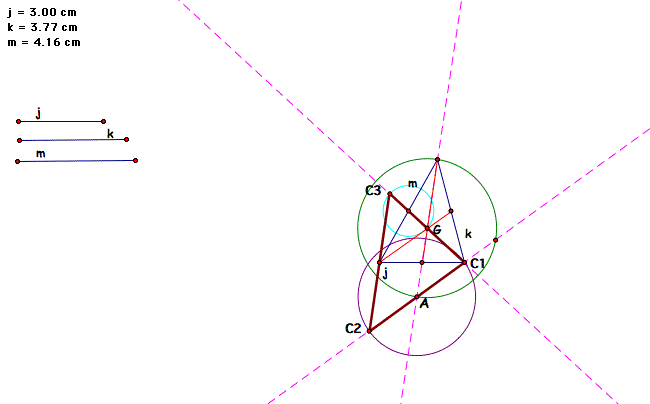
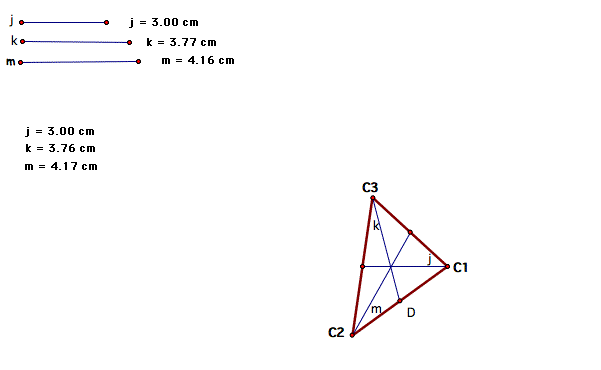
To check, we merely copy the triangle we made and then create its medians. Then we measure its medians and the medians we were given to see if they are correct.
By Carolyn Amos