ASSIGNMENT #9

PEDAL TRIANGLES AND THE SIMSON LINE

 

By: Katie Gilbert

Find all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle). This line segment is called the Simson Line.

As we begin to look at the relationship between the simson line and the pedal triangle, let's first define those two terms.

PEDAL TRIANGLE: Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.(click here to see a diagram in GSP, and you can move P around to see how the Pedal Traingle changes)

SIMSON LINE: In geometry, if one drops perpendiculars from a point P on the circumcircle of a triangle ABC to the sides (or their continuations) of the triangle, then the feet of the perpendiculars turn out to lie on a line, called the Simson line (of P for the triangle ABC - SEE DIAGRAM BELOW FOR ILLUSTRATION OF SIMSON LINE)

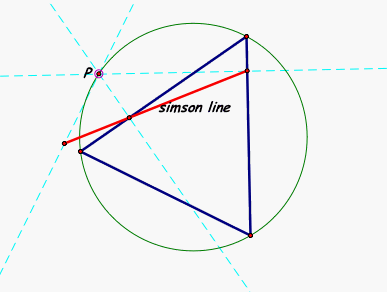
Now let's explore our Pedal Triangle and see if we can find when the three vertices of our Pedal Triangle are colinear, another words forms a degenerate triangle, and when this is equal to the simson line. The definition of the Simson line is a big clue, let's see if it is what we think..........

First let's take a look at P when it is inside the triangle:

You can see in our first image, that when our point P lies inside the triangle our pedal traingle is contained inside the original triangle.

But as we investigate further, we see that as we move our point P closer to the vertex of our triangle that our pedal triangle seems to start collapsing, looking more like a line. Let's see what happens if we put our point P on the vertex, are our suspisons correct??

We are correct, when our point P lies on one of the vertices of our original triangle, our pedal triangle, is degenerate, the vertices of our Pedal Triangle are colinear. Now let's see if it is the same as our Simson line...

We see that indeed our pedal triangle which has become degenerate, is indeed the same line as our Simson line.

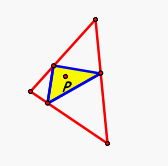
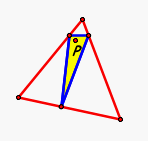
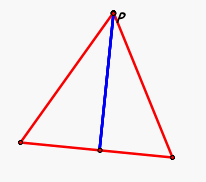
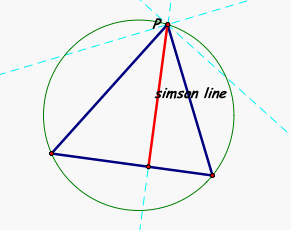
Now that we know that our Pedal Triangle is colinear and and forms the Simson line at each vertices (click here to explore this finding) we must see if there are other cases for P where this is also true. We have already checked for P inside the triangle, so now let's investigate for our point P outside the triangle......

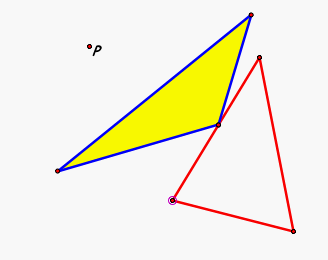
We see her that when our point P is outside our triangle that our pedal triangle is also outside our triangle, this makes sense by the definition of a pedal triangle it is where the vertices of the Pedal Triangle are formed by the perpindicular line dropped from to each side, OR EXTENSION OF A SIDE - which is the case here. Therefore our Pedal Triangle is formed outside our original triangle.

(CLICK HERE FOR BETTER UNDERSTANING, AND SEE DIAGRAM WHERE PERPINDICULAR LINES ARE SHOWN THAT FORM PEDAL TRIANGLE)

Now let's see if we can find if there exists any point P outside our triangle, where P would again create a Pedal Triangle where the vertices would be colinear, forming a degenerate triangle, and that line would be equal to our Simson Line.

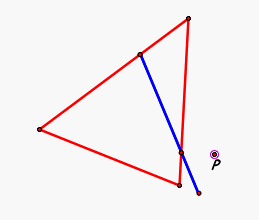
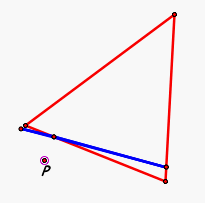
Here is one point where P creates a degenerate Pedal Triangle and is equal to the Simson Line.

And another, where the same holds.

Let's see if we can use what we know about our Simson Line and where we have found our points P where the vertices of our Pedal Triangle are colinear, form a degenerate triangle, and also form the Simson Line?

As I mentioned earlier our big clue in finding our answer involves the definition of the Simson Line, it states that it is formed by the perpindiculars from a point P that is ON THE CIRCUMCIRCLE of the triangle. So let's take the points we have found in our explorations above and see if they all fall on the circumcircle.

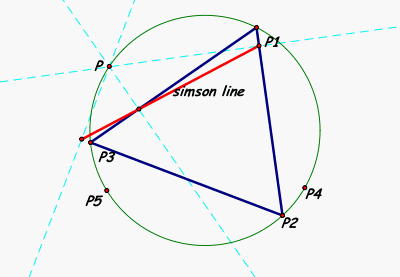
We see in our diagram above that our earlier explorations of different points P (P1, P2, P3, P4, P5) do all fall on the circumcircle, if we couple this with the definition of the Simson Line we can answer our initial question. Find all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle)........we can conclude that for any point P on the Circumcircle, when we construct the Pedal Triangle from this point P, the vertices of the Pedal Triangle will be colinear, forming a degenerate triangle, and the line formed by the vertices are the Simson Line.

CLICK HERE TO VARY POINT P ON THE CIRCUMCIRCLE TO DOUBLE CHECK OUR CONCLUSION (where P1, P2 and P3 are the vertices of the pedal triangle)

One interesting thing you might find when investigating the GSP diagram above, is that when our point P, on the cirucmcircle, and it's altitude is the perpindicular bisector of one of the sides of our original triangle, the simson line is equal to that side of the triangle.

 

RETURN