
Parametric
Investigations
by Molly McKee




Investigate
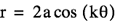
with varying a and k
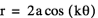
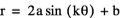
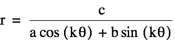
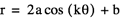
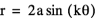
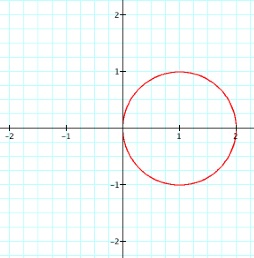
When a=1 and k=1, our graph looks like a circle which passes through the origin, but is contained in quadrants I and IV. So it looks just like the sine version, just rotated. This makes sense, since the sine graph and cosine graph are similar in the same way.
When a=1 and k=-1, our graph looks the same. We will find that this is always the case with this equation; the negative graph and positive graphs are identical.
When a changes the image gets larger or smaller, but retains the same general shape. Therefore we know that a is a scalar of the equation. The graph becomes more interesting as k fluctuates.
If k equals an even number, say 2, we can see that the graph again begins to look like a flower centered around the origin. The number of ‘pedals’ on the flower are still 2k, but the placement is different; in this graph the ‘pedals’ straddle the x-axis and the y-axis. The same differences and similarities can be found when k is odd and when k is a fraction.
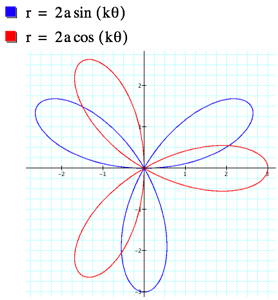
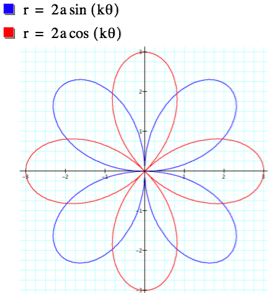
This equation is also a variation on a coil. The main difference between the cosine and sine version of the equations are the construction of the coil. When k=0 the, the cosine graph is a circle centered around the origin, whereas the sine graph is 0. This means that the coil created by the cosine graph begins from a circle.
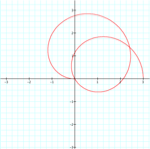
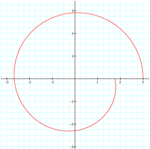
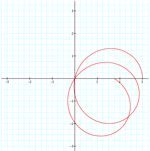
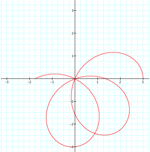
k = .15
a = 1.5
k = .75
a = 1.5
k = 1.15
a = 1.5
k = 1.35
a = 1.5
