In this exploration, we will investigate the polar equation r = a + b cos (kq) where a and b are real numbers, k is an integer, r is the radial coordinate which denotes the point's distance from a central point known as the pole (the origin in the Cartesian system), and q is the angular coordinate which denotes the counterclockwise angle required to reach the point from the polar axis (the x-axis in the Cartesian coordinate plane). Then we will compare this with the polar equation r = b cos (kq) for various k. Finally, we will see what happens if cosine is replaced by sine.
First, let's look at several graphs of r = a + b cos (kq) where a = b = 1 and k = 1, 2, 3, 4, and 5. This is one version of the "n-leaf rose." We will not overlay the graphs so that it is easier to see.
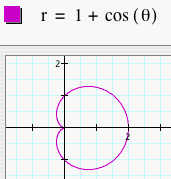
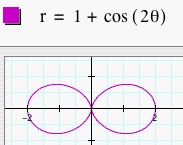
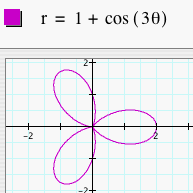
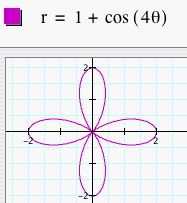
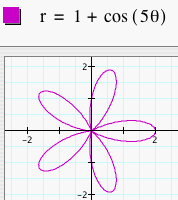
Notice that in each of these graphs, we let a = b = 1. When k = 1, the graph was a 1-leaf rose. When k = 2, the graph was a 2-leaf rose. As k changes, the number of leaves changes to k. So, if k = 8. we would get a 8-leaf rose. Click HERE to change k and observe the graphs. What happens when we change a and b to something other than 1 but keep them equal? Let's look at several graphs of r = a + b cos (kq) where a = b = 2 and k = 1, 2, 3, 4, and 5.
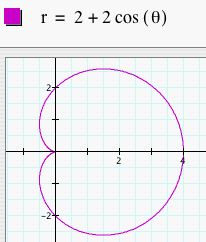
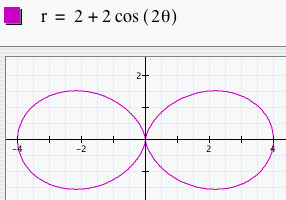
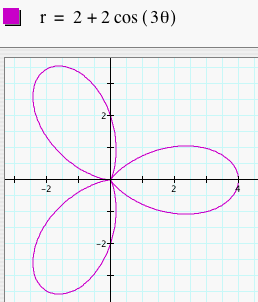
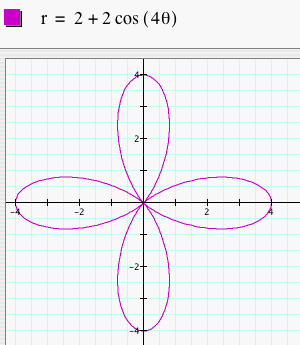
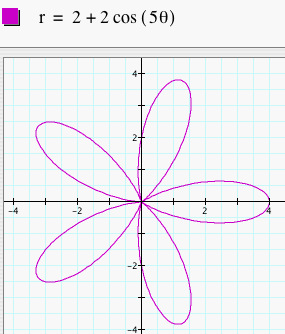
Notice that these graphs are similar to the above graphs, but these are just larger. These graphs are just dilations of the first set of graphs by a scale factor of a (or b since a = b). The number of leaves is still k. Click HERE to change a, b, and k (with a = b) and observe the graphs. Make sure to try a and b where they are not integers, but any real number.
Now, let's let a = 0 and graph the polar equation r = b cos (kq). How are these graphs different than r = a + b cos (kq)? Let's look at several graphs of r = b cos (kq) where b = 1 and k = 1, 2, 3, 4, and 5.
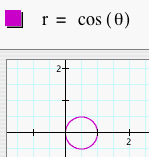
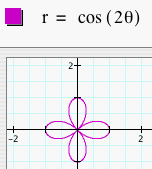
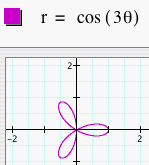
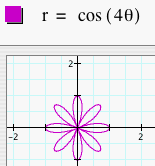
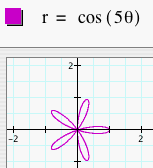
We see that when a = 0, the number of leaves is still dependent on k, but it is also dependent on whether k is even or odd. When k is odd, we get a k-leaf rose. When k is even, we get a 2k-leaf rose. We can predict that if k = 7, we will get a 7-leaf rose and if k = 8, we will get a 16-leaf rose. Click HERE to change b and k and observe the graphs. Let's look at several graphs of r = b cos (kq) where b = 2 and k = 1, 2, 3, 4, and 5.
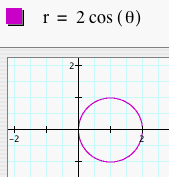
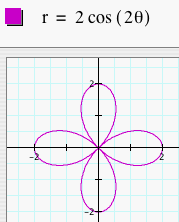
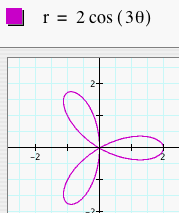
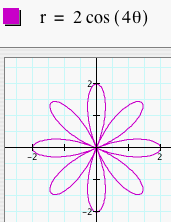
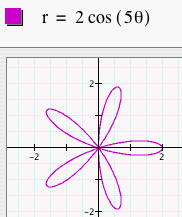
Again, we see that these graphs are similar to the set of graphs above, but these are larger. These graphs are dilations of the previous set of graphs by a scale factor of b. Now, let's explore what happens to the graphs when we replace cosine with sine.
First, we will look at the graphs of r = a + b sin (kq) where a = b = 1 and k = 1, 2, 3, 4, and 5. We have graphed these along with the previous graphs of r = a + b cos (kq) with the same a, b, and k values.
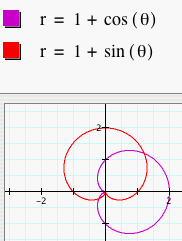
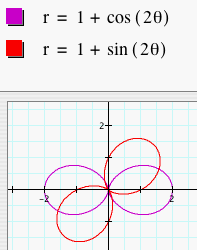
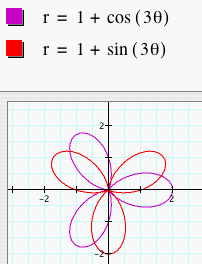
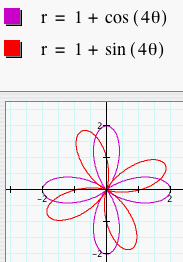
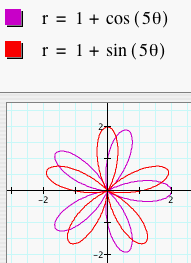
When cosine is replaced by sine, the graph
of the polar equations rotates by 
radians.
When k = 1, the graph rotates by 
radians. When k = 2, the graph rotates by 
radians.
When k = 3, the graph rotates by 
radians.
Following the pattern, the graph will rotate radians
when cosine is replaced with sine.
Again, if we change a and b and leave them equal, the only difference will be the dilation of the new graphs.
In this exploration, we restricted k to be an integer. Click HERE to further explore the graphs of the polar equations r = a + b cos (kq) and r = a + b sin (kq) where k is any rational number. Also explore when a and b are not equal (i.e. a < b or a > b). Click HERE to further explore the graphs of the polar equations r = b cos (kq) and r = b sin (kq) when k is any rational number. Also explore when a and b are not equal (i.e. a < b or a > b).