

There is no doubt that when teaching mathematics, we use graphs of functions to help make a point, to complete a problem, or to help students understand a new concept. The question then to ask is, should there be a whole presentation of multiple, different graphs or a sequence of those graphs? In which way will students better understand the material? To evaluate this problem, I tried to examine several cases in which multiple functions would be graphed in the classroom.
The first case I explored deals with varying the coefficient a of y=ax2. I graphed the following: y=-3x2, y=-2x2, y=-x2, y=x2, and y=2x2.
Initially I graphed all five functions at once to compare with graphing the five functions in sequence. Here is a view of the five functions all at once,
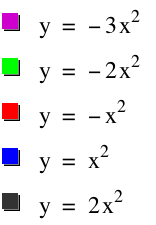

Now I would like to show a sequence of graphs consisting of the same functions.
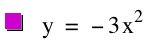
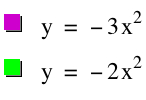
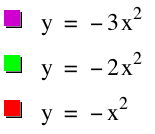
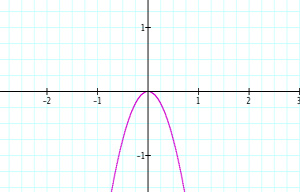
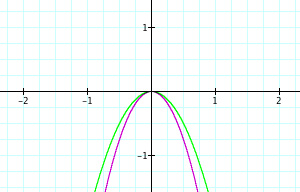
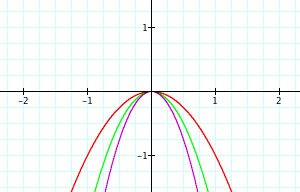
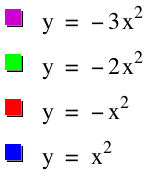
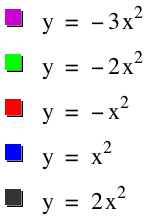
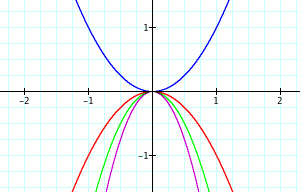
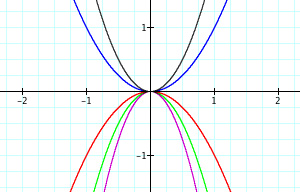
I believe in either this order or in another sequence, students can gain or learn concepts more effectively than when the graphs are presented all at once. Within the first three graphs, students can visualize how an increasing coefficient for a negative quadratic function expands the graph. As well, the students then see in the following two graphs what an increasing coefficent does for a positive quadratic function: squeezes the graph. In both cases (sequence or not), students will eventually gain this understanding about increasing and decreasing the coefficient, but the issue is how. When students are able to view graphs in a sequence, they have a greater chance of seeing the connection for themselves. Students can look at the progression of the graphs and make observations. After observations and some discussion, students are capable of making certain conclusions about what they saw within the graphs. What is important is that when students can teach themselves or make certain conclusions and inferences, the material is more important to them and stays with them for a longer period of time. This type of process for students is what we want to achieve. Let us look at another example of functions.
Now we want to look at five new functions: y=x, y=x2, y=x3, y=x4, and y=x5. Here is a graph of all functions at once,
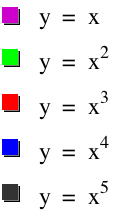

Now again, I want to look at the sequence or progression of these functions and their graphs.
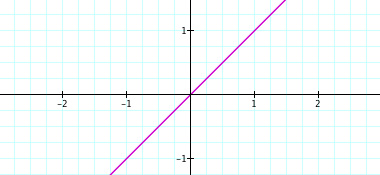
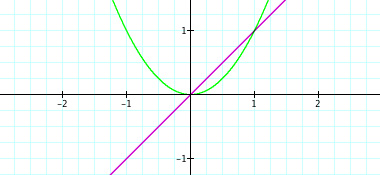
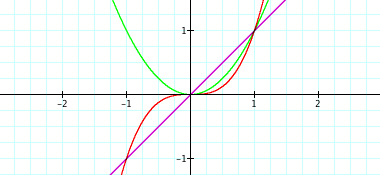
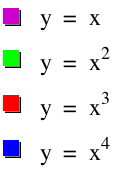
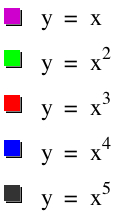
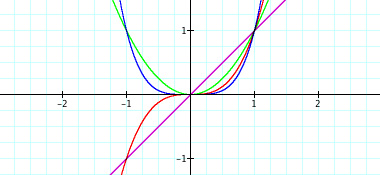
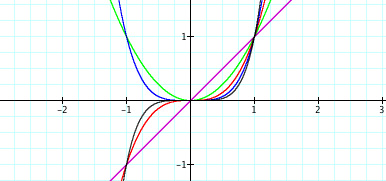
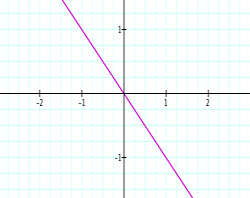
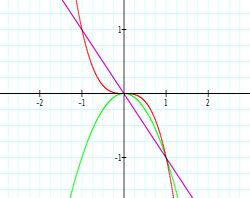
As you can see, when trying to explain certain properties about functions, graphing the functions in sequence can be very beneficial. The exponents of these polynomial functions alternate with each new graph--first odd, then even, then odd, and so on. When students are given this presentation of graphs, they may be able to make a connection with the even/odd exponents and the end behavior of each function. This type of conclusion or getting students to gather this concept may be rather difficult when looking at all five functions at the same time. From this point, a teacher might display five new functions of the same nature but with a leading coefficient of -1: y = -x, y=-x2, y=-x3, y=-x4, and y=-x5. These functions with looked similar. Again, students will recognize the same concepts from before, but hopefully notice the difference made by the negative coefficient. This difference can also be shown through a sequence of graphs. The sequence is shown below,

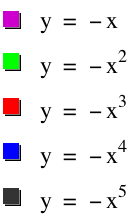
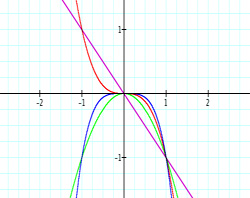
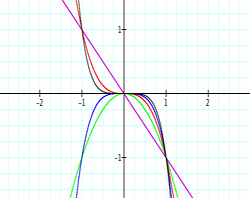
In conclusion, sequencing graphs in a particular order gives students the chance to derive, complete, or question concepts on their own. As presented in one bundle of graphs, students may not be able to make the connections necessary for full and beneficial learning. When students are seeking answers for themselves, teachers are not handing the information to them, where the students may not appreciate the material nor will they retain the material. We want students to make the connections on their own and sequencing the graphs of functions provides another useful outlet to make this happen.