

Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove:
HD/AD + HE/BE + HF/CF = 1 and AH/AD + BH/BE + CH/CF = 2.
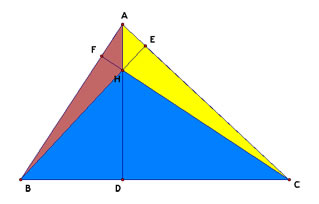
To prove these relationships, we will use area of triangles and ratios. First we will prove the relation equating to 1.
Proof:
We first note that triangle ABC must be acute; that is, any angle of the triangle must be less than or equal to 90°.
For triangle ABC, we know the area A = 1/2*BC*AD = 1/2*AC*BE = 1/2*AB*CF, where AD, BE, and CF are the altitudes to their respective bases. We will let A1 be the area of triangle BHC, A2 be the area of triangle AHB, and A3 be the area of triangle AHC, where H is the orthocenter of triangle ABC. Then, A1 = 1/2*HD*BC, A2 = 1/2*HF*AB, and A3 = 1/2*HE*AC. We know that the sum of the areas of these triangles is equal to the area of triangle ABC; thus, A = A1 + A2 + A3. If we divide through both sides with A, the area of the original triangle, then we have 1 = A1/A + A2/A + A3/A. Now we coordinate values of A based on the values of each area of the smaller triangles. Thus, A1/A = (1/2*HD*BC)/(1/2*BC*AD) = HD/AD. Next, A2/A = (1/2*HF*AB)/(1/2*AB*CF) = HF/CF. Lastly, A3/A = (1/2*HE*AC)/(1/2*AC*BE) = HE/BE. Thus, we have that 1 = HD/AD + HF/CF + HE/BE.
Now we much show that 2 = AH/AD + BH/BE + CH/CF. We already have that 1 = HD/AD + HF/CF + HE/BE. Note that HD = AD - HA, HF = FC - HC, and HE = BC - HB. Then we use these in substitution with the previously found relation. Therefore, 1 = (AD - HA)/AD + (FC - HC)/FC + (BE - HB)/BE = 1 - HA/AD + 1 - HC/FC + 1 - HB/BE = 3 - (HA/AD + HC/FC + HB/BE). Now we have that 1 = 3 - (HA/AD + HC/FC + HB/BE); hence, 2 = HA/AD + HC/FC + HB/BE.
QED