Jernita Randolph

Exploration of Parametric Curves

Let’s start with an observation of and for , when a=b.

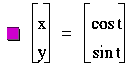
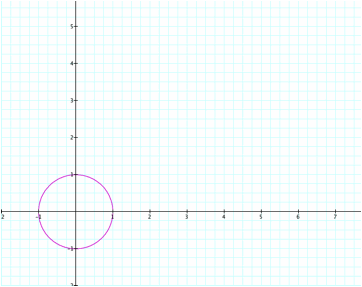
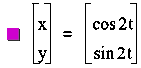
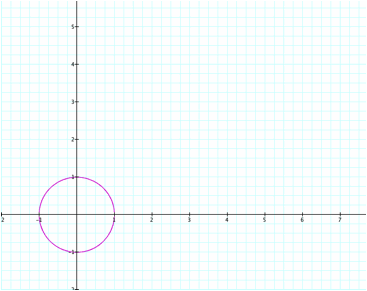
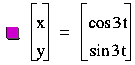
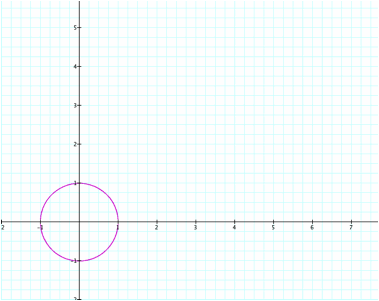
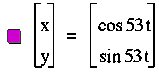
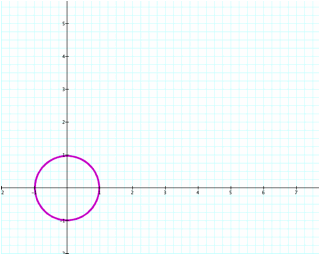
Notice that regardless of the integer value as long as a=b, we have a circle.

Next, let’s observe values where a ≤ b,

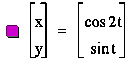
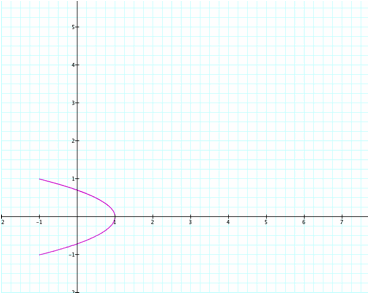
Here we have half a curve.

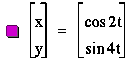
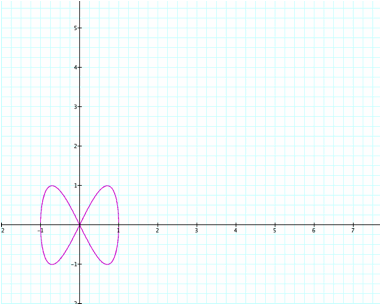
Here we have 2 loops.

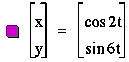
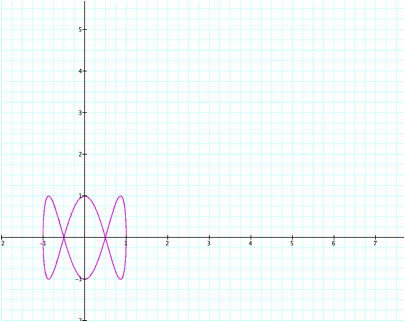
Notice a pattern?

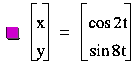
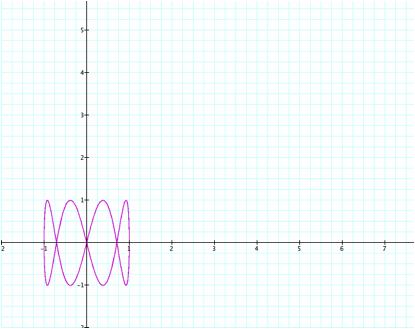
When a ≤ b the number of loops is 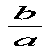with symmetry along the x-axis.

Now, let’s observe values where a ≥ b,

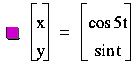
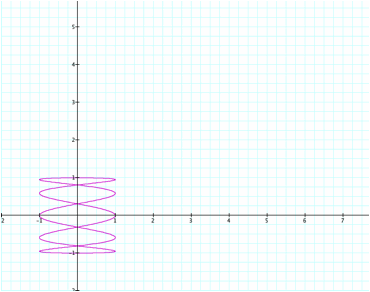
We have 5 loops with symmetry to the y-axis.

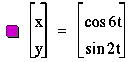
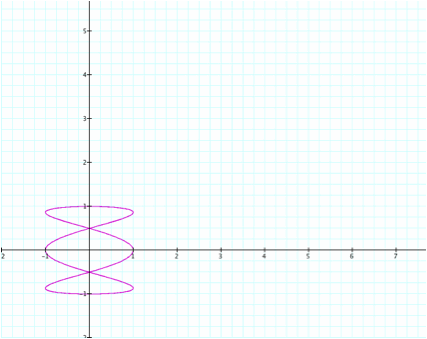
Here we have 3 loops with symmetry to the y-axis. The same pattern follows as with a ≤ b, except now the number of loops is equal to with symmetry to the y-axis.

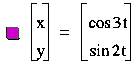
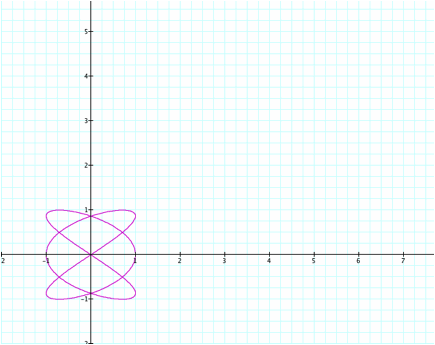
What happens when a is not evenly divisible by b? Here we have 3 loops with symmetry to the y-axis superimposed over 2 loops with symmetry to the x-axis.

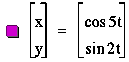
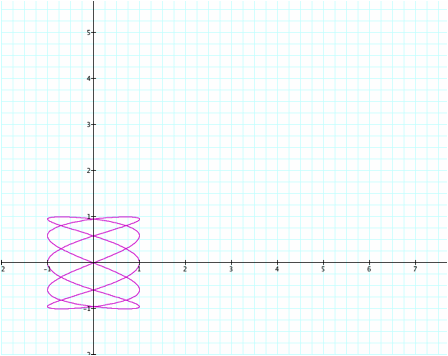
And here we have 5 loops with symmetry to the y-axis superimposed over 2 loops with symmetry to the x-axis.

Return